Zu a>0 seien
abgeschnittene Zylinder mit Länge 2a bzw. a. Wir betrachten in diesem Abschnitt das folgende Problem:
Der Gleichung (2.21) kommt folgende Bedeutung zu: Eine Lösung des Problems auf
dem unendlichen Zylinder ist maximal bestimmt bis auf Translation, d.h. wenn 
eine Lösung
ist, so auch 
für jedes 
. Bei der späteren Grenzwertbildung 
, d.h. beim Übergang von beschränkten Zylindern auf den unbeschränkten, muß
daher die Lösung an einem Punkt fixiert werden, um als Grenzwert keine konstante Funktion zu
erhalten. Die Gleichung (2.21) legt hierzu den ,,Beginn`` der Flammenfront an
die Stelle 
.
Zuerst stellen wir fest, daß jede 
-Lösung der Differentialgleichung gemäß Satz
5.8 automatisch von der Klasse 
ist. Dies
ermöglicht uns die problemlose Anwendung der Maximumprinzipien und der Monotonieaussagen aus Kapitel
.
Das Problem auf einem endlichen Zylinder soll mit Hilfe einer verallgemeinerten Kontinuitätsmethode gelöst werden. Dazu wird zunächst eine a priori-Abschätzung bewiesen:
BEWEIS.
Da u der Differentialungleichung 
genügt, folgt aus
dem Starken Maximumprinzip von E. Hopf: Falls u ein absolutes Minimum an einem Punkt innerhalb 
annimmt, so ist u konstant. Aufgrund der Randwerte (2.20) auf der rechten
und der linken Zylinderwand kann u aber nicht konstant sein und somit kein Minimum im Innern
annehmen. Für den Fall, daß u ein absolutes Minimum an einem Randpunkt 
annimmt, so besagt das Maximumprinzip ebenfalls, daß 
gilt. Aufgrund der
Neumannrandwerte (2.19) muß ein solches Randminimum auf dem
Dirichletrand 
liegen, so daß u>0 in folgt.
Falls es ein 
mit 
geben würde, so gäbe es aufgrund der
Stetigkeit eine Umgebung 
mit 
. Wegen 
ließe sich dann ebenfalls das Maximumprinzip anwenden, und man erhielte
einen Widerspruch. Also gilt 
auf 
.
Damit ist bereits eine 
-Schranke für u gefunden. Bevor diese zu einer 
-Schranke
ausgedehnt werden kann, wird eine Schranke für c benötigt. Betrachte dazu die folgenden
gewöhnlichen Differentialgleichungen für 
:
Dieses Randwertproblem ist eindeutig lösbar. Mit der Bezeichnung 
ersieht man aus
(2.18) und (2.23):
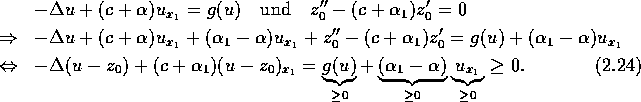
Hierbei haben wir uns die strenge Monotonie von u in 
-Richtung zunutze gemacht:
sie folgt aus Satz 3.1 des Kapitels 3 über Monotonie. Die strenge
Monotonie impliziert übrigens sofort 0<u<1 in 
.
erfüllt die Bedingungen des Starken Maximumprinzips von E. Hopf, also besitzt v kein inneres Maximum, es sei denn
v ist konstant. Das Maximum liegt nicht auf dem Neumannrand 
, falls
v nicht konstant ist, denn sonst müßte in einem solchen Punkt 
gelten, was die homogene
Neumannrandbedingung 
aber ausschließt. Daher wird
das Maximum auf dem Dirichletrand angenommen, also
und somit
Analog dazu erhält man über die Ungleichung
eine obere Abschätzung für 
durch 
, es gilt also
Rechnet man 
und 
explizit aus, so erhält man
Daraus ersieht man
Weil u monoton wachsend in -Richtung ist, nimmt u den Wert 
aus der Gleichung
(2.21) für an. Daher ergibt sich aus (2.29)
Daraus läßt sich folgendermaßen eine Schranke für |c| herleiten (vgl. dazu auch die Abbildung):
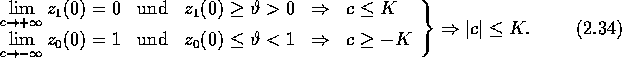
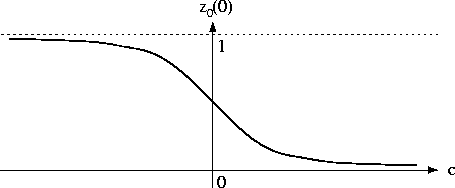
Die Konstante K hängt dabei von und ab, diese Funktionen wiederum von a, 
,
und M.
Mit Hilfe der -Schranke für u und der Schranke für |c| läßt sich nun aus dem Kapitel
5 über elliptische Abschätzungen eine -Schranke für u herleiten: Für
beliebiges p>1 gibt es gemäß Satz 5.7 eine Konstante 
, die
nur von n, p, 
, a, , und M abhängt, so daß gilt:
Wegen 
und 
ist die rechte Seite beschränkt durch 
. Mit
Hilfe des Sobolewschen Einbettungssatzes läßt
sich aus der -Abschätzung leicht eine -Abschätzung gewinnen: Wähle p>n, dann gilt
mit einer Konstanten 
, die nur von , a, n und p abhängt. Somit folgt unmittelbar
die gewünschte -Abschätzung für u:
BEWEIS. Zum Beweis dieses Lemmas wird eine modifizierte Kontinuitätsmethode verwendet. Konkret
bedeutet das, daß die Lösung (u,c) ein Fixpunkt eines Operators 
sein wird, dessen
Existenz über die Lösungseigenschaft des Leray-Schauderschen Abbildungsgrades garantiert wird. Um zu
zeigen, daß der Abbildungsgrad von null verschieden ist, werden zwei Homotopien verwendet. Die erste
,,verbiegt`` den Operator zu einem leicht handhabbaren Operator 
, und die
zweite diagonalisiert diesen zu einem Operator 
. Der Abbildungsgrad des Operators
läßt sich dann leicht mit Hilfe des Produktsatzes bestimmen.
Zu 
, 
und 
seien
Offenbar ist (u,c) eine Lösung des Problems (2.18) -
(2.21), wenn (u,c) Fixpunkt von bzw. Nullstelle von 
ist.
Sei K die Konstante aus der a priori-Abschätzung (Lemma 2.2), mindestens jedoch so groß, daß
Setze
Zeige nun, daß der Leray-Schaudersche Abbildungsgrad 
definiert ist,
d.h. daß 
eine kompakte Störung der Identität ist und daß 
auf 
gilt. Beachte, daß auf B die 
-Topologie zugrunde gelegt
wird.
Zum Beweis der Kompaktheit von 
muß gezeigt werden, daß 
präkompakt
ist. Hierzu bedienen wir uns wieder der -Abschätzung aus Satz
5.7 und des Sobolewschen Einbettungssatzes:
Die 
-Norm von 
ist beschränkt, da wie mit früherer Argumentation gemäß dem
Maximumprinzip 
gilt. Also ist 
gleichgradig
stetig. Der Satz von Arzela-Ascoli garantiert
nun die Präkompaktheit dieser Menge, d.h. 
ist eine kompakte Abbildung. Daraus folgt
unmittelbar, daß kompakt ist und damit eine kompakte Störung der
Identität ist.
Weiterhin gilt auf , denn aus 
folgt,
daß (u,c) eine Lösung des Problems (2.18) - (2.21) ist.
Gemäß der a priori-Abschätzung Lemma 2.2 folgt 
und 
, jedoch liegt (u,c) nur dann auf , wenn 
oder |c|
= K+1 gilt.
Nachdem nun gezeigt ist, daß der Abbildungsgrad wohldefiniert ist, muß noch nachgewiesen werden, daß
auch stetig ist. Dazu nehmen wir an, daß 
eine Folge ist, die
gegen 
konvergiert, wobei die Konvergenz der 
wieder in der -Topologie zu
verstehen ist. Sei 
. Mit der gewohnten -Abschätzung
folgern wir wie in (2.35), daß die 
in der -Norm beschränkt sind. Weil
beschränkte Teilmengen von schwach folgenkompakt sind, gibt es eine Teilfolge, die schwach gegen ein 
konvergiert. Da die gemäß dem Sobolewschen Einbettungssatz auch in der 
-Norm
beschränkt sind, sind deren Gradienten gleichgradig stetig. Nach dem Satz von Arzela-Ascoli sind die
präkompakt bzgl. , durch nochmaligen Übergang zu einer Teilfolge erreicht man also, daß
die in gegen 
konvergieren. Weil die eine Seite 
der Differentialgleichung somit in gegen 
konvergiert, so konvergiert auch 
in gegen eine Funktion 
.
Da die in schwach gegen 
konvergieren, gilt 
, und
ist Lösung der Differentialgleichung zu . Da die Lösung des linearen Problems
eindeutig ist, muß 
gelten. Mit der gleichen Argumentation erhält man, daß
jeder Häufungspunkt der ursprünglichen Folge die eindeutige Lösung ist, d.h. es gibt genau
diesen einen Häufungspunkt, und die ganze Folge konvergiert gegen . Also
sind und damit auch 
stetig. Aus der eindeutigen Lösbarkeit und der a priori-Abschätzung konnte
also die Stetigkeit gewonnen werden.
Die Homotopieinvarianz des Abbildungsgrades liefert uns daher
Untersuche nun : Die Lösung der Differentialgleichung 
von
(2.38) für 
ist (analog zu den Lösungen und )
Bemerke, daß 
nur von und nicht von y abhängt, die Elimination des einzigen von y
abhängigen Terms 
in der Differentialgleichung führt also dazu, daß sich die partielle
Differentialgleichung wie eine gewöhnliche verhält. Dies wird freilich erst durch die homogenen
Neumannrandbedingungen auf 
ermöglicht. Da 
eine
bijektive Abbildung 
ist, legt die Fixpunktgleichung c fest:
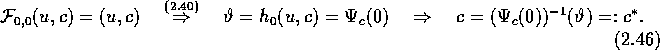
Das nun feste 
erlaubt die Definition der zweiten Homotopie: Zu ,
und 
seien
Wie oben kann man nachweisen, daß diese Homotopie zulässig ist und somit gilt:
Der Operator
ist nun diagonalisiert, d.h. die erste Komponente 
des Bildbereichs hängt nur
von u ab, und die zweite Komponente 
nur von c. Dies ermöglicht die
Anwendung des Produktsatzes:
Wegen 
besitzt die erste Abbildung im Produkt den Grad +1. Wegen
(2.41) gilt 
und 
, so daß die zweite Abbildung den Grad -1 besitzt. Somit gilt
Die Lösungseigenschaft des
Abbildungsgrades garantiert nun die Existenz einer Nullstelle von und damit einer Lösung
(u,c) des Problems (2.18) - (2.21).
