In diesem Abschnitt wird der Grenzübergang 
durchgeführt, wozu wir zunächst
eine a priori-Abschätzung für c benötigen, diesmal jedoch unabhängig von a.
BEWEIS.
Die Existenz einer solchen Konstante, die von a abhängt, wurde bereits in Lemma
2.2 gezeigt. Zur Abschätzung nach unten verfahren wir wie dort:
Für die Lösung 
der gewöhnlichen Differentialgleichung (2.23) zeigt man
mit Hilfe des Maximumprinzips die Ungleichung 
. Daraus folgt die Ungleichung
. Da 
als Funktion von 
monoton fällt
und 
bijektiv auf (0,1) abbildet, folgt die Schranke 
. Für
ergibt sich daraus
Zur Abschätzung nach oben kann man nicht genauso mit 
statt 
verfahren, da 
nicht
als Funktion von darstellbar ist (siehe explizite Darstellung
(2.31) von ). Betrachte stattdessen die Lösung
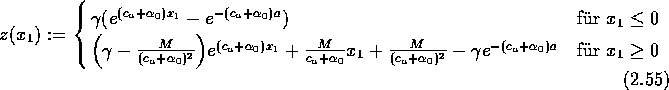
der gewöhnlichen Differentialgleichung
wobei H die Heavyside-Funktion ist, d.h. 
, 
.
Wir nehmen dabei an, daß 
ist; ansonsten ist eine a priori-Schranke bereits
gegeben. Wählt man
so erfüllt z die Randwerte z(-a)=0 und z(a)=1. Man rechnet nach, daß z stetig
differenzierbar ist, und sieht leicht, daß z außer im Punkt 
beliebig oft differenzierbar
ist. Mit dem üblichen Maximumprinzip-Argument von oben sieht man wegen 
leicht
ein. Hierbei ist zu beachten, daß das Maximumprinzip trotz des kleinen
Regularitätsmangels in 0 anwendbar ist, denn falls u - z dort ein Maximum annimmt, so folgt
(das gilt für beliebige 
-Funktionen) und 
rechts- und
linksseitig getrennt, denn 
. Insbesondere folgt 
, also
Setze die Definition von 
ein und schätze ab:
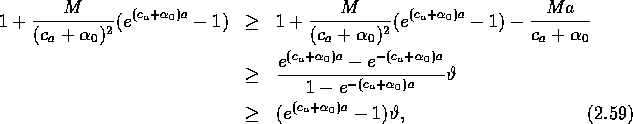
also
Falls 
sein sollte, so folgt
und somit 
, was äquivalent zu 
ist. Da nach Voraussetzung ist, liefert uns dies die von a unabhängige Schranke
Mit Hilfe der von a unabhängigen a priori-Abschätzung läßt sich nun durch Grenzübergang eine Lösung finden:
BEWEIS. Da nach Lemma (2.4) c unabhängig von a beschränkt
ist, garantiert die bereits mehrfach verwendete 
-Abschätzung Satz
5.7 wie vorhin, daß die -Normen der Funktionen 
auf
jedem Teilgebiet der Form 
beschränkt sind, diesmal jedoch
unabhängig von a. Das heißt, daß es ein K gibt, so daß für alle a und 
gilt:
Weil beschränkte Teilmengen von schwach folgenkompakt sind
, gibt es zu jedem solchen Teilgebiet eine Folge 
, so daß 
dort schwach in gegen ein 
konvergiert. Da die
gemäß Lemma
2.4 beschränkt sind, kann man durch Übergang zu einer Teilfolge
erreichen, daß die zugehörigen gegen ein c konvergieren.
Mit Hilfe des Sobolewschen Einbettungssatzes folgt aus der -Abschätzung
Gemäß dem Satz von Arzela-Ascoli sind diese Funktionen daher präkompakt bzgl. der -Norm
auf jedem solchen Teilgebiet, also konvergiert nach erneutem Übergang zu einer Teilfolge 
in dem Teilgebiet bezüglich der -Norm gegen ein 
. (Die Grenzwerte der
schwachen -Konvergenz und der -Konvergenz stimmen überein.) Die genügen der
Differentialgleichung 
. Weil die rechte
Seite in 
gegen 
konvergiert, tut dies auch die linke Seite, so daß
u der Differentialgleichung 
genügt.
Wegen 
und 
in 
ergibt sich weiterhin 
und 
in 
.
Von nun an sei mit (u,c) stets ein solcher Grenzwert gemeint. Gemäß Satz
5.8 gilt 
.
BEWEIS.
Auf 
gilt 
und somit g(u)=0. Daher genügt es, das erste Integral auf
zu betrachten. Für beliebiges z>0 gilt
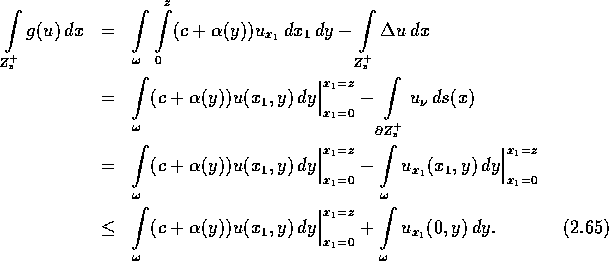
Hierbei wurde verwendet, daß die Normalenableitung von u auf 
verschwindet
und daß ist. Wegen 
und 
ist das erste
Integral der letzten Zeile unabhängig von z nach oben beschränkt. Durch den Grenzübergang 
erhält man die Endlichkeit von 
.
Durch Multiplikation der Differentialgleichung (2.8) mit u vor der
Aufintegration erhält man analog die Endlichkeit von 
:
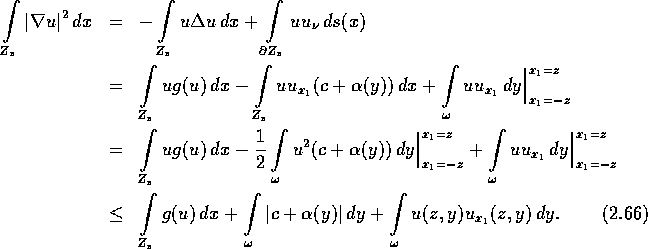
Die beiden ersten Summanden der letzten Zeile sind unabhängig von z beschränkt, es bleibt also noch die Untersuchung des letzten. Weil
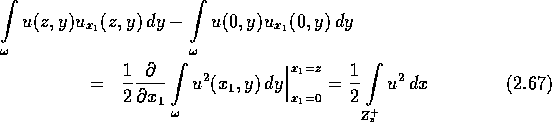
monoton in z ist, ist auch 
monoton in z. Daher ist dieser
Term entweder beschränkt oder er konvergiert gegen 
für 
. Falls er
gegen konvergiert, so müßte dies aber auch für 
gelten, was
wegen der Beschränktheit von u jedoch ausgeschlossen ist. Also ist unabhängig von z beschränkt.
BEWEIS.
Da u beschränkt und monoton in 
-Richtung ist, existieren die Limites
Zu 
setze
Für beliebige 
erfüllt 
die Differentialgleichung 
, also gilt gemäß der gewohnten
-Abschätzung 5.7
denn 
für 
. Also konvergiert
in 
nicht nur bezüglich der -Norm, sondern auch bezüglich der -Norm. Weil
wie in Lemma 2.6
gezeigt endlich ist, muß 
gelten, d.h. 
sind Konstanten. Da
auch das Integral endlich ist, muß 
gelten. Wegen
, 
und 
folgt 
oder 
.
BEWEIS.
Sei . Die Monotonie in -Richtung von u impliziert und
wegen (2.13) 
. Integriere die Differentialgleichung
(2.8) über das Gebiet 
und betrachte die Grenze 
. Weil 
wie eben gezeigt für 
gleichmäßig in
y gegen 0 konvergiert, folgt
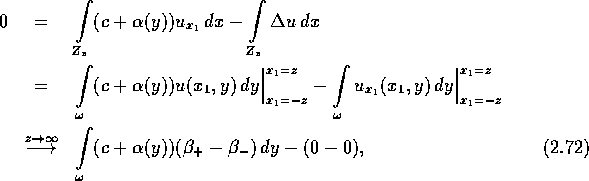
und somit
Falls man die Differentialgleichung vorher mit u multipliziert, folgt analog
Der zweite Summand auf der linken Seite ist ein Vielfaches von (2.73), also folgt
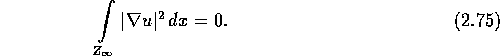
Also ist u konstant und 
.
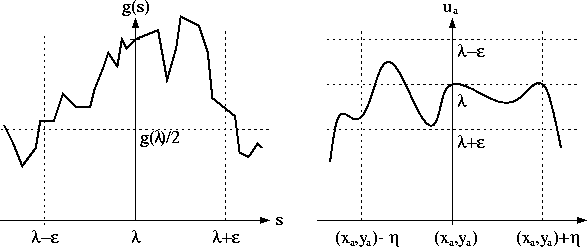
BEWEIS.
Wähle 
beliebig. Aufgrund der Stetigkeit von g gibt es ein 
mit 
. Zu jedem gibt es ein
und ein 
mit 
. Setze 
. Wegen 
, K unabhängig von a, folgt für 
die Abschätzung 
(vgl. dazu auch die Abbildung).
Aufgrund der Glattheit des Randes von 
gibt es ein von unabhängiges 
,
so daß 
gilt. Damit folgt
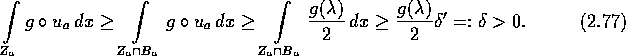
BEWEIS.
Gemäß Lemma 2.7 können nur die beiden Fälle
und auftreten. Wir untersuchen beide Fälle getrennt.
Fall 1: . Integriere die Differentialgleichung (2.18) für
die Funktion über dem Gebiet 
auf:
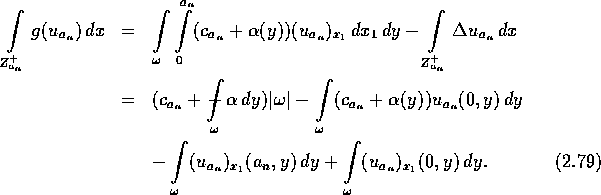
Aus Lemma 2.5 wissen wir, daß in der
-Norm kompakt gegen 
konvergiert. Also konvergiert der drittletzte Summand gegen
und der letzte gegen null. Wegen 
kann der zweitletzte Summand weggeschätzt werden, und nach Lemma
2.9 gilt
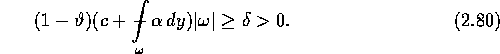
Wegen 
folgt nach Division durch 
die Behauptung.
Fall 2: . Mit einer Rechnung analog zum Beweis von Lemma
2.8 erhält man
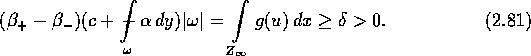
Nun soll der Fall ausgeschlossen werden. Dies geschieht durch den Vergleich
von u mit einer Funktion 
, die das asymptotische Verhalten von u modelliert. Sie wird
mittels verallgemeinerter Eigenwert- und Eigenfunktionverfahren aus dem Kapitel 4
gewonnen.
BEWEIS.
Aufgrund von Lemma 2.10 ist es möglich, ein mit
und 
für hinreichend große a zu finden. Gemäß Satz
4.1 gibt es eine strikt positive Funktion 
und
einen verallgemeinerten Eigenwert 
, so daß gilt:
Da 
nur bis auf eine multiplikative Konstante bestimmt ist, können wir 
auf 
annehmen. Mit
gilt
Wegen und folgt auf 
:
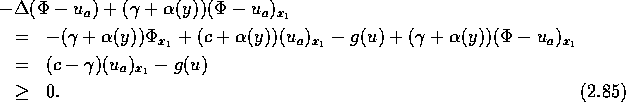
Wegen und (2.83) folgt
Mit Hilfe des gewohnten Maximumprinzips folgt nun 
und somit
auf . Wegen 
folgt 
.
Wie bereits oben gezeigt können höchstens die Fälle und
auftreten. impliziert und ist somit ausgeschlossen.
Demnach bleibt nur und übrig, was Gleichung (2.9)
zeigt.
Wir haben also bis hierhin die Existenz einer Lösung von
(2.8)-(2.10) gefunden. Da u als Grenzwert von
Funktionen mit gewonnen wurde, folgt . Mit dem Maximumprinzipargument
von Lemma 2.2 folgt 0<u, also ist die Ungleichung
(2.14) gezeigt. Leider läßt sich auf diesem Weg nicht eine Ungleichung u<1
zeigen, denn in einer Umgebung eines Maximums 1 ist g(u) i. allg. nicht konstant null und besitzt
das falsche Vorzeichen zur Anwendung des Maximumprinzips.
Da die Funktionen streng monoton wachsend sind, folgt für die Grenzfunktion u sofort die
Ungleichung (2.15), und das Theorem ist bewiesen.
