Gegeben sei ein beidseitig unendlicher Zylinder, in dem sich ein brennbares Gasgemisch befindet. Zur Beschreibung der Verbrennungsvorgänge dieses Gasgemisches gibt es zahlreiche mehr oder weniger zutreffende Modelle. Ein sehr allgemeines und umfassendes ist im Anhang von [BL] auf Seite 37 beschrieben. Da es jedoch aus vielen hinsichtlich der Form wesentlich verschiedenen Einzelgleichungen besteht, die sich wiederum aus vielen unterschiedlichen Variablen wie Druck, Dichte, Geschwindigkeitsfeld, Temperatur und Massenanteil des Frischgases zusammensetzen, entzieht es sich aus Komplexitätsgründen einer analytischen Behandlung. Daher wird das Modell folgendermaßen vereinfacht:
Die ,,isobare Approximation`` geht davon aus, daß der Druck des Gasgemischs überall und zu jedem Zeitpunkt konstant ist. Diese Einschränkung ist sinnvoll, da sich Flammenfronten i. allg. mit einer Geschwindigkeit ausbreiten, die unterhalb der des Schalls liegt, und daher die bei der Verbrennung entstehenden Druckwellen sich von der enstehenden Flammenfront entfernen und keinen Einfluß auf die weitere Verbrennung haben. Weiterhin verwendet man die ,,Konstante-Dichte-Approximation``, die das Modell so lange nicht in unzulässiger Weise beeinträchtigt, wie die Reaktions-Diffusions-Effekte die hydrodynamischen dominieren, was z.B. bei hinreichend gleichmäßigen Gasströmungen der Fall ist. Beide Approximationen führen uns zu folgendem System:
Hierbei sei
der beidseitig unendliche Zylinder; das Gebiet 
sei beschränkt und habe
einen 
-Rand für ein beliebiges 
. Wir nehmen 
an, da eine
kleinere Raumdimension eine Entartung bedeuten würde. Für einen Punkt 
schreiben wir
mit 
und 
. Die Funktion u = u(x, t) bezeichnet die auf
[0,1] normalisierte Temperatur des Gasgemischs an der Stelle x zum Zeitpunkt t. Analog dazu
bezeichnet v = v(x, t) den Massenanteil des Frischgases im Zylinder. v=1 bedeutet, daß nur
frisches Gas vorliegt, während v=0 besagt, daß alles Gas verbrannt ist. 
bezeichnet
die künstlich aufgeprägte Grundgeschwindigkeit des Gases parallel zu der Zylinderwand; das
Geschwindigkeitsfeld 
ist divergenzfrei. Die positive
Konstante Le ist die ,,Lewis-Zahl``, in die verschiedene physikalische Konstanten eingehen. Sie
wird hier als Le=1 angenommen und findet daher keine weitere Berücksichtigung. Zuletzt bezeichnet
f(u) das Maß des chemischen Verbrennungsvorgangs.
Bei der Verbrennung entsteht eine Flammenfront, die sich im Zylinder ausbreitet. Wir interessieren
uns hier nur für ,,travelling-wave-solutions`` dieses Systems, d.h. wir nehmen an, daß sich die
Flammenfront mit konstanter Geschwindigkeit in 
-Richtung ausbreitet. Daher betrachten wir nur
Lösungen der Form 
bzw. 
. Die Konstante c bezeichnet dabei die
Ausbreitungsgeschwindigkeit der Flammenfront und darf als Unbekannte als eine Art ,,Eigenwert``
angesehen werden. Mit diesem Ansatz wird aus dem parabolischen System (2.1)
das elliptische System
Als Randwerte legen wir fest:
Hierbei bezeichnet das nach unten gestellte 
die Ableitung in Normalenrichtung
. Die Gleichung (2.4) legt fest, daß die
Zylinderwand keinen Einfluß auf die Verbrennung nimmt. Die Gleichungen (2.5) und
(2.6) sind als Grenzwert zu verstehen und besagen, daß sich in Richtung
als Grenzwert nur frisches Gas und in Richtung 
nur verbranntes Gas befindet; die
Verbrennung verläuft also von nach .
Zwischen den Funktionen u und v besteht ein direkter Zusammenhang:
BEWEIS.
Sei w:=u+v. Die Funktion 
ist eine stetige Abbildung der
kompakten Menge 
nach 
, wobei
vereinbart sei. 
nimmt dort also sowohl Minimum als
auch Maximum an. Liegen diese beiden Extrema in 
, so gilt
wegen 
, und das Lemma ist bewiesen.
Ansonsten besitzt w ein Extremum in 
. Da w die Differentialgleichung
erfüllt, folgt aus dem Starken Maximumprinzip von E. Hopf
, daß w keine inneren Extrema besitzt, es sei denn w ist konstant. Das
Extremum kann aber nicht auf dem Rand 
liegen, denn
dann müßte an diesem Punkt nach Theorem 7 aus [PW] 
gelten, die
äußere Normalenableitung von w ist aber null. Somit bleibt nur der Fall 
. 
Daher kann man v durch 1-u ausdrücken und die zwei Gleichungen des Systems (2.3) auf eine reduzieren. Mit der Bezeichnung g(u) := (1-u) f(u) ergibt sich
mit den Randbedingungen
An die Koeffizienten stellen wir die Forderungen
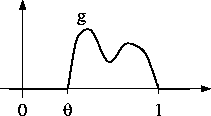
Die Konstante ist bereits von der Randglattheit 
her bekannt. Unter diesen Voraussetzungen beweisen wir in den Fällen n=2 und n=3
das Hauptresultat:
Theorem: Für alle den Bedingungen (2.11)-(2.13)
genügenden Funktionen
und g gibt es eine Lösung 
des Problems (2.8)-(2.10). Für die
Lösung gilt:
Im Fall n > 3 gilt die Aussage vermutlich auch, jedoch gibt es im Beweis eine Lücke, die selbst
nach langer Arbeit nicht geschlossen werden konnte: Es fehlt der Schluß, daß Lösungen der Klasse
automatisch von der Klasse sind. Ausführliche Bemerkungen und
Begründungen dazu finden sich in Kapitel 
.
Die prinzipielle Vorgehensweise ist die folgende: Im Abschnitt 2.2 wird die Existenz einer Lösung eines ähnlichen Problems auf beschränkten Zylindern gezeigt. Im Abschnitt 2.3 betrachtet man dann behutsam den Grenzübergang für immer größer werdende Zylinder und erhält so eine Lösung des Problems auf dem unbeschränkten Zylinder.
