Sei 
ein beschränktes Gebiet mit 
-Rand, und sei b>0 eine reelle
Konstante. In dem Gebiet
betrachten wir die quasilineare Differentialgleichung
wobei f = f(x, z, p) stetig in der Variablen x, lokal Lipschitzstetig in z, p und monoton
wachsend in 
für 
sei. Als Randbedingungen fordern wir
Dann gilt
BEWEIS. Zu 
setze
Wir zeigen, daß für zwei Lösungen 
und 
auf
gilt:
Setzt man 
, so folgt daraus unmittelbar die strenge Monotonie. Ebenfalls folgt für zwei
beliebige Lösungen aus Stetigkeitsgründen 
und wegen der Vertauschbarkeit von u und
die Eindeutigkeit.
Nun zum Beweis von (3.7). Es gilt
Für 
folgt 
, weil f nach Voraussetzung monoton wachsend in
ist, insbesondere gilt auch 
. Für 
ist f(x,z,p) nach Voraussetzung lokal
Lipschitzstetig in z und p. Da die beiden Funktionen und v -Funktionen auf einer
kompakten Menge sind, sind die Argumente x, v(x) und 
kompakt und f dort global
Lipschitzstetig. Die Lipschitzkonstante 
hängt dabei natürlich von v ab. Wegen folgt
Setze
Wir haben damit eine Funktion 
mit 
gefunden, so daß
gilt. Damit erhalten wir die Differentialungleichung
Diese linearisieren wir wie folgt:
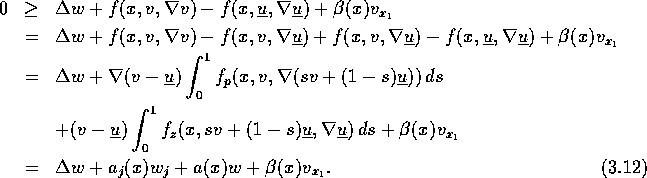
Die Schreibweise der Differenzen als Integrale ist aus folgendem Grund möglich: Da f in den
Variablen z und p lokal Lipschitzstetig ist, ist die Funktion 
aus 
. Gemäß Satz A5.5 aus [Alt], Seite 185 ist 
. Setze 
. G läßt sich durch 
-Funktionen bzgl. der
-Norm approximieren, d.h. es gibt eine Funktionenfolge 
mit 
in ; automatisch gilt 
in 
. Damit
folgt:
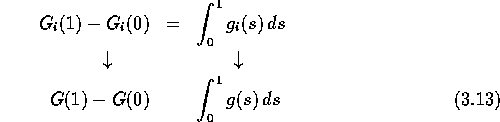
Die andere Umformung wird analog gerechtfertigt.
Setze
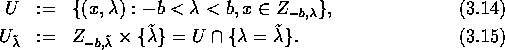
Falls 
eindimensional ist, d.h. n=2 gilt, hat U folgendes Aussehen:
Wegen 
erhalten wir in U die Differentialungleichung
Für 
gilt aufgrund der Randbedingungen
(3.3) und (3.4) 
oder 
. Daher folgt für hinreichend kleine 
aus Satz 3.5
auf 
. Nach Voraussetzung des Satzes gibt es zu ein 
, so daß 
ist. Daher folgt aus Satz
3.7 w>0 in .
Sei 
die größte Zahl, für die noch für alle 
gilt. Wie
gerade erörtert gilt 
. Wir möchten 
zeigen.
Annahme: 
. Dann gibt es Folgen 
und 
mit
. Die 
können so gewählt werden, daß w auf 
sein
Minimum annimmt und somit 
gilt. Durch Übergang zu einer Teilfolge
erreicht man, daß die gegen ein 
konvergieren. Aus Stetigkeitsgründen
folgt 
. Wie oben gibt es zu ein , so daß 
ist. Aus Satz 3.7 folgt w>0 in 
, so daß 
nicht im Inneren
liegen kann. Aus Satz 3.6 folgt 
, so daß
aus dem Dirichletrand stammen muß. Es gilt also:
Fallunterscheidung:
mit 
:
Aus Satz 3.6 folgt 
, Widerspruch zu 
.
mit :
Aus Satz 3.6 folgt 
, Widerspruch zu .
mit 
und 
:
Aus Satz 3.8 folgt 
oder 
. Beides steht im Widerspruch zu (3.17).
Da alle drei Fälle zum Widerspruch führen, muß die Annahme falsch sein, und es folgt die
Behauptung. 
