Im letzten Abschnitt wurde vorausgesetzt, daß der Rand des Gebiets glatt ist, damit er von einem Diffeomorphismus auf ein Hyperebenenstück glattgebogen werden kann. Unter bestimmten Voraussetzungen lassen sich die Abschätzungen jedoch auch auf nichtglatte Gebiete verallgemeinern, und zwar mit Hilfe von Spiegelungstechniken. Gegeben sei folgende Situation:
Das Gebiet
ist das cartesische Produkt eines endlichen Intervalls 
mit 
und
eines beschränkten Gebiets 
mit 
-Rand. Offenbar ist 
ohne weiteres nicht glatt genug für die Abschätzungen des letzten Abschnitts, denn der Rand ist
lediglich von der Güte 
. Auf 
ist eine Funktion u gegeben, die einer
Differentialgleichung mit Randbedingungen der folgenden Art genügt:
Auf wird dann eine 
-Abschätzung für u wie in den vorherigen Abschnitten
benötigt. Da die Abschätzung des vorherigen Abschnitts nur für glatte Gebiete gilt, wird die
Funktion u über den Rand von hinaus mittels einer Spiegelung fortgesetzt, in der
Hoffnung, daß die gespiegelte Funktion auf dem erweiterten glatten Gebiet selbst glatt ist und einer
glatten Differentialgleichung genügt. Dabei gibt es zwei grundlegende Möglichkeiten: a) Fortsetzung
mittels einer ungeraden Spiegelung über den Dirichletrand 
hinaus,
und b) Fortsetzung mittels einer geraden Spiegelung über den Neumannrand 
hinaus.
Die Technik a) kann freilich nur funktionieren, wenn u auf den Spiegelachsenrandstücken
konstant ist, was in unserer Anwendung jedoch kein Problem ist: Entweder ist die Funktion dort
konstant 0 oder 1, oder sie ist schon auf einem etwas größeren Gebietsstück gegeben, so daß sich
eine Spiegelung ganz erübrigt. Für den linken Rand 
und u=0 dort hat die
Spiegelung dann folgende Form:
Die Spiegelung am rechten Rand mit u=1 erfolgt analog. Bei dieser ungeraden Spiegelung bleibt die
Differentialgleichung erhalten, lediglich das Vorzeichen des Koeffizienten 
ändert sich. Dies
führt zu einer Unstetigkeit in diesem Koeffizienten, die für die 
-Abschätzungen jedoch nicht
von Bedeutung ist. Insofern erhält man mit dieser Methode -Abschätzungen, jedoch keine
Schauderabschätzungen. Diese sind aber sowieso nicht zu erwarten, denn die ungerade Spiegelung ist
lediglich eine 
-Fortsetzung, so daß die Funktion u über die Spiegelungskante hinweg
i. allg. nicht zweimal stetig differenzierbar sein wird, zumindest solange 
dort nicht
verschwindet.
Daher verwerfen wir die Technik a) und widmen uns der Möglichkeit b), nämlich der Spiegelung am
(i. allg.) gebogenen Neumannrand. Der gebogene Rand muß zunächst auf ein Hyperflächenstück
geradegebogen werden. Dazu genügt es, wenn wir die 
-Koordinate zunächst außen vor lassen.
Da das Gebiet 
einen -Rand besitzt, gibt es zu jedem Punkt 
eine Umgebung 
, eine offene Menge 
mit 
und einen
-Diffeomorphismus
Die Koordinaten aus V bezeichnen wir mit 
. Wir erweitern 
zu einer
Funktion 
vermöge
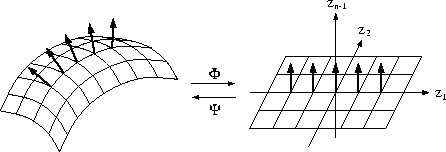
Nach eventueller Verkleinerung von U und V ist 
ein -Diffeomorphismus.
Diese Konstruktion ist in der Differentialgeometrie unter dem Namen ,,Fermi-Koordinaten``
bekannt
. Würde man stattdessen gleich von einer
abstrakten Funktion ausgehen, die U diffeomorph nach V abbildet, so erhielten wir keine
Orthogonalitätsbeziehungen, die jedoch unbedingt erforderlich sind, wie wir später sehen werden.
Sei 
die Inverse von . Wir betrachten nun die Differentialgleichung unter
der Transformation 
. Sei 
die transformierte Funktion. Dann gilt
Die Randbedingungen transformieren sich erwartungsgemäß:
d.h. Normalenableitungen gehen wieder in Normalenableitungen über.
Wir untersuchen das Aussehen der Matrix 
, und zwar
durch Betrachtung ihrer Inversen 
. Dies ist
tatsächlich die Inverse, denn
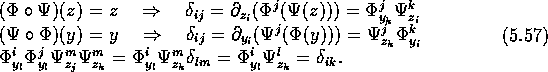
Weil 
tangentiell zu 
im Punkt 
für alle 
ist und 
senkrecht dazu liegt, gilt
also
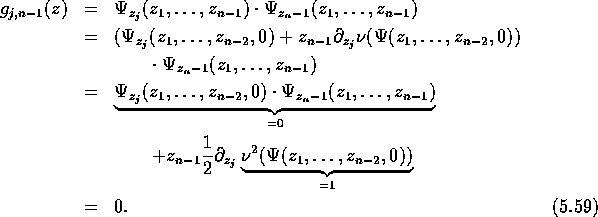
Da die Matrix symmetrisch ist, ergibt sich die Gestalt
Damit hat auch ihre Inverse 
diese Gestalt. Dies erlaubt
uns die Herleitung von -Abschätzungen:
BEWEIS. Dieser Satz wird ähnlich bewiesen wie Satz 5.6, unterschiedlich ist lediglich die Behandlung des Randes. In Satz 5.6 wurde zu jedem Punkt aus dem Inneren des Gebiets eine ganz im Inneren liegende Umgebung gefunden und dort eine innere lokale Abschätzung verwendet, ebenso wurde zu jedem Randpunkt das Gebiet lokal glattgebogen und mit einer Randabschätzung abgeschätzt. Ein Kompaktheitsargument lieferte dann die Abschätzung für das ganze Gebiet. Für diesen Satz dagegen wird folgendermaßen verfahren:
Für jeden inneren Punkt des Gebiets finden wir wie gehabt eine lokale Abschätzung, ebenso wird für
jeden Punkt aus dem glatten Rand eine lokale Randabschätzung
durchgeführt, was problemlos ist, wenn man die Umgebung so klein wählt, daß man von den Ecken im
Gebietsrand wegbleibt. Neu ist die Behandlung der Punkte aus 
.
Zu jedem solchen Punkt kann das Gebiet wie oben beschrieben lokal glattgebogen werden, die
-Koordinate bleibt ohne Transformation bestehen. Wie man den Transformationsgleichungen
(5.55) und (5.56) entnimmt, genügt die glattgebogene
Funktion v dann einer Differentialgleichung
mit der Randbedingung 
. Mittels der Vorschrift
wird v gespiegelt. Dabei ändern sich die Vorzeichen der Ableitungen 
,
, 
, 
, 
. Die Koeffizienten der Terme
zweiter Ordnung der Differentialgleichung bleiben erhalten, denn die Matrix 
hat wie
vorher festgestellt an den Stellen, wo die Ableitungen das Vorzeichen wechseln, eine Null
stehen. Das heißt, daß die gespiegelte Funktion der Differentialgleichung
(5.62) genügt, deren Koeffizienten zweiter Ordnung stetig sind. Daher lassen
sich auch hier lokale -Abschätzungen finden, und zwar innere, falls der Ursprungspunkt aus
stammt, und Randabschätzungen, falls der Punkt aus
stammt (den ursprünglichen Gebietsecken), wobei dann der
verbleibende Rand der (gerade) Dirichletrand ist, denn der Neumannrand wurde soeben durch
Spiegelung unschädlich gemacht. Da die Integralnormen der Funktion auf dem Spiegelgebiet gleich den
Integralnormen auf dem ursprünglichen Gebiet sind, folgt am Ende mittels des Kompaktheitsarguments
die gewünschte -Abschätzung auf . 
Mit dieser Methode lassen sich auch Schauderabschätzungen durchführen, solange man weiß, daß alle Koeffizienten der Differentialgleichung Hölderstetig sind.
BEWEIS.
Anstelle der -Abschätzungen werden Schauderabschätzungen verwendet, ansonsten wird genauso wie
in Satz 5.7 verfahren. Hierbei muß jedoch garantiert werden, daß die
Koeffizienten nach der Spiegelung noch Hölderstetig sind. Konkret wird als innere Abschätzung Satz
6.2 oder Korollar 6.3 aus [GT] und als Randabschätzung Korollar 6.7 verwendet
werden.
Im Fall n=2 tritt das Problem der Randglattheit nicht auf, da ein Intervall ist und keine
Spiegelung erforderlich ist. Im Fall n=3 bedienen wir uns eines Resultats aus der
Differentialgeometrie. Schreibt man die Transformation des Laplaceoperators beim Glattbiegen
mittels der Christoffelsymbole auf, so ergibt sich gemäß [Ham] (Seite 4), daß 
übergeht in
ist dann als eindimensionale Mannigfaltigkeit lokal eine Kurve, durch die wir eine
Geodätische laufen lassen und so unsere Funktion erhalten. Zu dieser Geodätischen bilden wir
wie in Gleichung (5.54) die Fermikoordinaten. Gemäß einem Resultat aus
[GKM] (Seiten 113-114) verschwinden dann die Christoffelsymbole entlang der
Geodätischen: 
. Damit fallen die Terme erster Ordnung, die durch den
Laplaceoperator entstehen, auf dem Gebietsrand weg. Da die Differentialgleichung nach Voraussetzung
ebenfalls keine Terme erster Ordnung in y- bzw. z-Richtung enthält, entstehen hier auch keine
Unstetigkeiten. Die Terme zweiter Ordnung wurden bereits vorher als stetig erkannt; für die
Hölderstetigkeit gilt das gleiche. Somit erhält man nach der Spiegelung eine Funktion, die einer
Differentialgleichung mit hölderstetigen Koeffizienten genügt, so daß die Anwendung der lokalen
Schauderabschätzungen möglich ist. Wie 5.7 wird durch ein
Kompaktheitsargument die Schauderabschätzung auf dem ganzen ungespiegelten Gebiet ermöglicht.
Im Fall 
verschwinden die Christoffelsymbole i. allg. nicht, so daß mit Unstetigkeiten
gerechnet werden muß, die die Durchführung der Schauderabschätzungen verhindern. An dieser Stelle
liegt die Lücke der Diplomarbeit, die trotz vieler Bemühungen und Forschungen in verschiedene
Richtungen leider nicht geschlossen werden konnte.
