Gemäß dem Verschiebungssatz 6.2 können wir durch hinreichend weite
Verschiebung von u nach links, d.h. hinreichend große Wahl von s, erreichen, daß 
ist. Verschiebe nun u soweit wie möglich zurück, d.h. wähle
Von nun an sei mit s stets dieses fest gewählte s gemeint.
BEWEIS. Wir nehmen an, daß die Aussage falsch ist, also z>0 in 
gilt. Betrachte die
asymptotischen Darstellungen von z für 
:
Die Summanden mit den Resttermen konvergieren für gegen null. Falls
c'>c ist, so gilt 
und die Terme B und C konvergieren gegen
0. Die verbleibenden Terme A und D sind strikt positiv, so daß man sieht, daß eine etwas
kleinere Wahl des Parameters s nicht die Nichtnegativität von z für betragsmäßig hinreichend
große 
gefährdet. Da nach Annahme z>0 in ist, wäre s somit nicht minimal,
d.h. der Fall c'>c kann nicht auftreten.
Betrachten wir also nun den Fall c'=c, d.h. 
, 
, 
und
. A, B, C und D sind dann unabhängig von . Weil 
und 
strikt
positiv sind, können A+B und C+D nur entweder strikt negativ, strikt positiv oder konstant null
sein. A+B und C+D sind aber keinesfalls negativ, denn sonst könnte nicht z>0 gelten. Falls
beide Terme strikt positiv wären, so wäre mit dem Argument von oben s nicht minimal. Somit folgt,
daß mindestens einer der beiden Terme verschwindet, d.h.
OBdA führen wir nur den Fall 
zum Widerspruch -- der andere wird
analog behandelt.
erfüllt die Differentialgleichung
denn 
und u' erfüllen die Differentialgleichung (6.1), und durch Subtraktion
dieser Gleichungen voneinander und beidseitigem Hinzufügen der rechten Seite von
(6.28) erhält man (6.28). Da f eine 
-Funktion im
zweiten Argument ist, läßt sich f um 1 in eine Taylorreihe entwickeln und das Lagrangesche
Restglied mit der Hölderbedingung abschätzen. So erkennt man, daß die rechte Seite von der
Größenordnung 
ist für 
. In den Kapiteln 2 und 4 von [BN1] wird die asymptotische Darstellung
mit Konstanten 
und 
gezeigt. Wir linearisieren den rechten Teil der
Differentialgleichung (6.28):
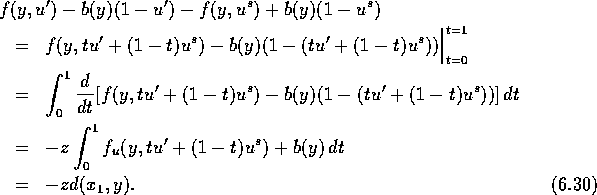
z erfüllt also eine lineare Differentialgleichung
Wende Lemma 4.3 aus [BN1] an: Für alle 
gibt es ein E>0, so daß für 
gilt:
Für 
sieht man, daß 
in (6.29) sein muß.
Andererseits erkennt man 
aus (6.26), denn es gilt ja und damit auch C+D=0. Dies ist ein Widerspruch, also muß die Annahme falsch
sein. Damit ist bewiesen, daß z an einer Stelle aus den Wert 0 annimmt. 
