Mit diesen Vorbereitungen können wir uns jetzt den 
-Abschätzungen zuwenden. Zunächst betrachten
wir den Fall eines elliptischen linearen Operators L, der nur Terme zweiter Ordnung mit konstanten
Koeffizienten enthält, d. h.
mit 
. Für 
-Funktionen ( 
) lassen sich dann auf
folgendem Weg die untenstehenden -Abschätzungen herleiten:
läßt sich die
Funktion u als Faltung von 
mit der Fundamentallösung von 
darstellen. Die
Calderon-Zygmund-Ungleichung gibt uns dann die Möglichkeit, 
über 
abzuschätzen.
in den Operator L aus Gleichung
(5.19).
und entsprechend
abgeschätzt.
-Abschätzungen in Verbindung mit Dirichletrandwerten werden auch von Gilbarg und Trudinger
[GT] (Kapitel 9) betrachtet. Die Behandlung allgemeiner Randwerte, auch der hier
benötigten homogenen Neumannrandwerte, ist jedoch wesentlich aufwendiger. Da
[ADN] genau die benötigten Abschätzungen bereitstellt, werden wir sie hier
zitieren. Zunächst aber zu der inneren Abschätzung, die wir vollständig beweisen.
BEWEIS. Im Fall n=1 ist die Behauptung trivial. Im Fall 
sei zunächst 
. Sei
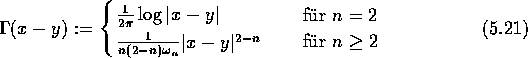
die Fundamentallösung der Laplacegleichung . Hierbei bezeichnet 
das Volumen des Einheitsballes im 
. Gemäß der Greenschen Darstellungsformel läßt sich u darstellen als
Faltung von mit 
:
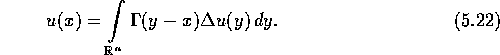
Da nach Voraussetzung 
ist, sind die Voraussetzungen der
Calderon-Zygmund-Ungleichung
erfüllt, und es folgt sofort die Behauptung.
Falls L nicht der Laplaceoperator ist, so kann eine lineare Abbildung gefunden werden,
die ihn zu transformiert, denn die
Koeffizienten von L sind konstant. So erhält man die Behauptung auch für den allgemeinen Operator
L, wobei durch die Transformation zusätzlich der kleinste und der größte Eigenwert der Matrix
in die Konstante C eingehen, d.h. C ist auch von 
und k abhängig. 
Eine ähnliche Abschätzung gilt für Funktionen auf einer Hemisphäre, die auf dem geraden Randstück
Neumannrandbedingungen genügen:
Dieser Satz wird hier nicht bewiesen; er entspricht Satz 14.1 aus [ADN] (Seite 701).
