Bei den Abschätzungen in diesem Kapitel werden wir die folgende Interpolationsungleichung benötigen:
Die Aussage dieses Satzes erhält man leicht für p=2 mittels partieller Integration. Die Aussage
für beliebiges p beweisen wir jedoch anders mit einer Methode von Nirenberg. Dieser beweist die
Ungleichung
zwar ebenfalls nur für den Fall p=2, der Beweis läßt sich jedoch verallgemeinern:
BEWEIS. Es genügt, die Aussage nur für Funktionen 
zu beweisen, da diese
Funktionen dicht in 
liegen und die Aussage des Satzes durch einfache Approximation
folgt.
Der Beweis erfolgt in drei Schritten: zuerst wird die Ungleichung für den eindimensionalen Fall
n=1 bewiesen, dann wird sie auf achsenparallele Würfel im 
ausgedehnt, und
schließlich werden allgemeine Gebiete behandelt.
Zunächst sei also n=1, d.h. 
ein endliches Intervall. Zu 
, das später
gewählt wird, unterteile in Teilintervalle, deren Länge mindestens 
beträgt, maximal jedoch 
. Dazu kann 
ggf. verkleinert werden, falls zu klein ist, was für die
Aussage nicht relevant ist, da dann eine schärfere Abschätzung bewiesen wird. Sei nun I=(a,b) ein
solches Intervall. Mit 
gilt dann folgende Relation, die wir später benötigen
werden:
Das Intervall I unterteilen wir weiter in vier gleichlange Teilintervalle der Länge 
, das
linke bezeichnen wir mit 
und das rechte mit 
. Seien 
und 
. Dann gibt es dem Mittelwertsatz gemäß ein 
, so daß gilt:
Damit gilt für beliebiges 
:
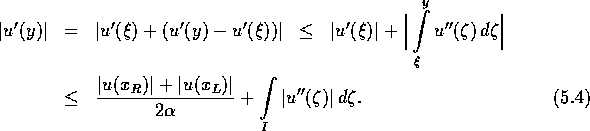
Integriere diese Ungleichung in den Variablen 
und 
über 
bzw. 
:
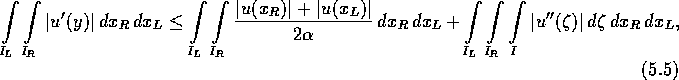
also
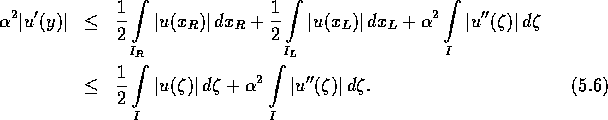
Dividiere dies durch 
, erhebe es zur p-ten Potenz und schätze mittels Hölderungleichung
ab:
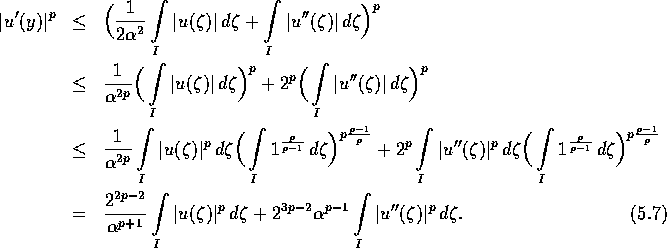
Integriere diese Ungleichung in der Variablen y über I:
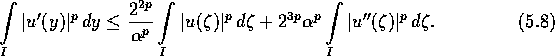
Nutze nun die Relation (5.2):
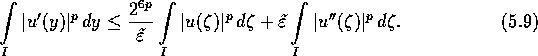
Summiert man über alle Teilintervalle I von , so folgt mit 
:
Das Ergebnis für den eindimensionalen Fall läßt sich leicht für Würfel 
verallgemeinern: Für jedes 
und für jedes 
mit 
gilt gemäß
(5.10):
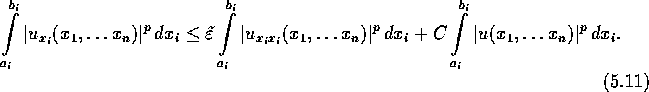
Integriere diese Ungleichung in den Variablen 
über das
n-1-dimensionale Gebiet 
:
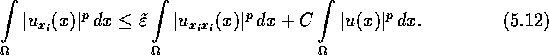
Summiere über 
auf. Wenn man dann noch 
über
abschätzt und einen 
-Term addiert, folgt für Würfelgebiete
:
Mit diesem Ergebnis können wir uns beliebigen beschränkten Gebieten 
mit 
-Rand zuwenden.
Die Randglattheit ermöglicht es, zu jedem 
eine Umgebung 
mit 
und einen -Diffeomorphismus 
zu finden, wobei 
eine offene Menge ist. Wir können 
und
in der Form verkleinern, daß ein achsenparalleler Würfel ist. Zu jedem 
sei weiterhin 
ein achsenparalleler Würfel, ebenfalls mit . Da
kompakt ist, gibt es eine endliche Menge 
mit 
. Da die endlich vielen Diffeomorphismen 
und 
für 
gleichmäßig beschränkt sind, gibt es eine Konstante k>0, die nur von
und I abhängt, so daß für i=0, 1, 2 gilt:
Also transformiert sich die oben bewiesene Abschätzung auf Würfelgebieten zu
Sei nun 
eine Oberschranke für die Zahl der Umgebungen , 
, die sich in
einzelnen Punkten aus überlappen. K ist durch 
majorisiert, i. allg. wird
K jedoch wesentlich kleiner sein. Es folgt
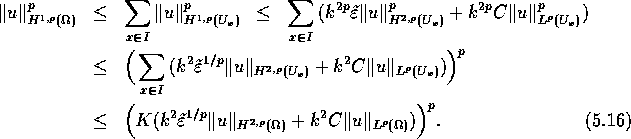
Mit der Wahl 
folgt die Behauptung.
Hinweis: Mittels Induktion läßt sich der Satz leicht erweitern zu
für ganzzahlige Konstanten j > i > 0. Ebenso lassen sich anstelle der vollen Normen 
auch Seminormen 
verwenden. Eine andere Beweismöglichkeit
ergibt sich durch die Nutzung des Ehrling-Lemmas (siehe [Alt]).
Als weiteres Hilfsmittel müssen zur Formulierung einer Randwertaufgabe die Randwerte von Funktionen
aus Sobolewräumen charakterisiert werden. Hierzu eignen sich am besten die sog. ,,fractional order
spaces``, das sind Sobolewräume 
mit nichtganzzahligem m. Die Einführung dieser Räume ist
aufwendig und würde den Rahmen dieser Arbeit sprengen, sie ist aber für unsere Zwecke auch nicht
erforderlich. Hier genügt es zu wissen, daß für hinreichend glatte
Gebiete die Randwerte von Funktionen aus 
gerade den
Funktionen aus 
entsprechen. Auf ist
eine Norm gegeben durch
Die Bedingung 
kann nicht als normale Gleichheit fast überall
aufgefaßt werden, da 
Nullmenge in ist und somit keine Einschränkung an
gemacht würde. Vielmehr gibt es eine stetige surjektive Abbildung 
, die für 
-Funktionen genau der Restriktion auf den Rand
entspricht, und mit
ist lediglich 
gemeint.
