Institute for
Numerical Simulation

Research Group
M. Griebel

• Home
• Publications
• Research
  • Projects
  • Software
  • Computing
  • Conferences
• Teaching
• People
• Miscellany
• Jobs
• Links
• Contact
• Inside

Parabolische Maximumprinzipien

 

Sei ein Gebiet mit für ein festes . Einen Punkt aus dem bezeichnen wir mit (x,t), wobei und ist. In diesem Abschnitt verwenden wir folgende Bezeichnungen:

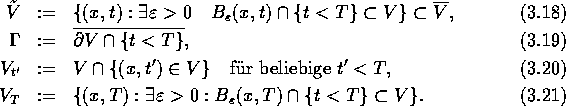
Ferner setzen wir voraus, daß die Mengen für alle zusammenhängend sind. Die Funktion sei zweimal stetig differenzierbar in den Variablen und einmal stetig differenzierbar in der Variablen t. Sie genüge in V der Differentialungleichung

 

 

 

BEWEIS. Seien R der Radius und der Mittelpunkt von B. OBdA sei P der einzige Punkt auf , an dem w den Wert M annimmt. Ansonsten gehe zu einem kleineren Ball B' über mit und . Wegen w<M in B folgt dann w<M in . Fahre dann mit B' statt B fort.

Sei . Nach Voraussetzung ist . Sei ein Ball mit Mittelpunkt P und Radius , wobei so klein gewählt ist, daß

Setze

 

Wegen w<M auf der kompakten Menge C' gibt es ein mit

Setze

Damit gilt

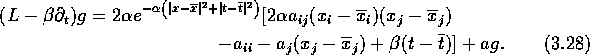
Nach Wahl von gilt für : . Daher kann so groß gewählt werden, daß

Setze

dann gilt . Wegen auf C' kann so klein gewählt werden, daß v<M auf C' ist. Wegen g=0 auf folgt v<M auf , v(P)=M. Die Funktion v nimmt ihr Maximum auf nicht innerhalb von D an, denn sonst müßte an einem solchen Punkt

gelten, was ein Widerspruch wäre. Also nimmt v sein Maximum auf einzig und alleine in P an, und somit gilt

Eine einfache Rechnung ergibt

und somit

Bemerkung: Die Aussage bleibt richtig, falls anstelle von ein beliebiger nach außen zeigender Vektor verwendet wird, d.h. ein Vektor mit . Dabei muß jedoch beachtet werden, daß der Differenzvektor von P und dem Mittelpunkt des Balles nicht parallel zur t-Achse liegen darf (Bedingung im Beweis).

 

BEWEIS. Seien R der Radius und der Mittelpunkt von B. OBdA sei P der einzige Punkt auf , an dem w den Wert M annimmt, ansonsten kann B wie im Beweis von Satz 3.2 verkleinert werden.

Annahme: mit , d.h. die Tangentialebene an B durch P liegt nicht senkrecht zur t-Achse.

Sei ein Ball mit Mittelpunkt P und Radius , wobei so klein gewählt ist, daß

zerfällt in die beiden Sphärensegmente

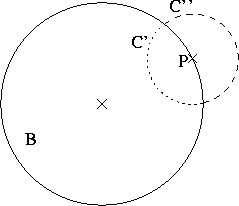
Wegen w<M auf der kompakten Menge C' gibt es ein mit

Setze

Damit gilt

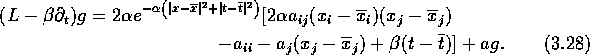
Nach Wahl von gilt für : . Wie im vorherigen Beweis kann so groß gewählt werden, daß

Mit

gilt . Wegen auf C' kann so klein gewählt werden, daß v<M auf C'. Wegen g<0 und auf C'' gilt v<M auf C'' und somit auf . Wegen g=0 auf gilt v(P)=w(P)=M, also nimmt v sein Maximum an einem inneren Punkt an. Dies ist ein Widerspruch:

Daher ist die Annahme falsch und die Behauptung bewiesen.

 

BEWEIS. Annahme: Es gibt einen Punkt mit .

OBdA sei so gewählt, daß w<M auf , d.h. daß es auf der Verbindungsstrecke von nach keinen weiteren Punkt gibt, an dem w den Wert M annimmt. Es kann angenommen werden, daß die Verbindungsstrecke vollständig in liegt, denn es gibt zumindest einen Polygonzug, der die beiden Punkte miteinander verbindet, wovon mindestens eine Teilstrecke die gewünschten Eigenschaften hat. Setze

und bezeichne

den Abstand des zu x nächstgelegenen Punktes, an dem w den Wert M annimmt. Für mit gilt wegen

 

Aus Lemma 3.3 folgt, daß ein solcher Punkt nur über oder unter x bezüglich der t-Achse liegen kann, also oder . Daher kann man mit Hilfe des Satzes von Pythagoras d für einen anderen Punkt auf der Verbindungslinie nach oben und nach unten wie folgt abschätzen, vgl. dazu auch die Zeichnung.

  

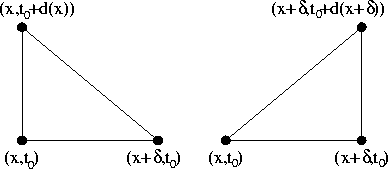
Der rechte Teil der ersten Abschätzung ist leicht einzusehen, wenn man ihn quadriert. Für einen Vektor entlang der Verbindungsstrecke und eine beliebige natürliche Zahl gilt damit

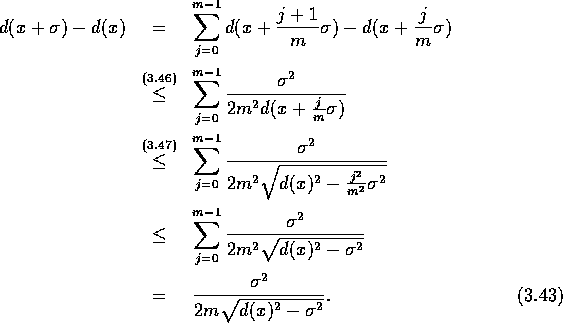
Lassen wir m gegen konvergieren, so folgt, daß d monoton fällt. Wegen (3.45) muß sein auf . Insbesondere folgt dort , was ein Widerspruch zu Wahl von ist.

Im folgenden sei ein weiterer kürzerer Beweis von Lemma 3.4 angegeben, der Satz 3.2 benutzt, aber dafür auf Lemma 3.3 verzichtet. Die Methode stammt von Berestycki und Nirenberg aus dem Beweis von Satz 3.7.

BEWEIS. (Zweiter Beweis von Lemma 3.4)

Sei mit der Eigenschaft, daß die Verbindungsstrecke in enthalten ist. Wir möchten zeigen. Dann folgt w<M auf , denn weil zusammenhängend ist, läßt sich jeder Punkt aus über einen polygonalen Streckenzug mit verbinden, und durch iterierte Anwendung folgt die Behauptung.

Sei so klein gewählt, daß w<M in und .

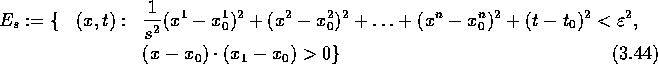
bezeichne ein Halbellipsoid mit Mittelpunkt .

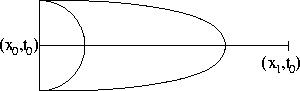
Nach Wahl von gilt w<M auf . Lasse nun s wachsen, solange w<M auf , maximal jedoch bis an stößt, d.h.  .

Annahme: Es gibt ein mit . Weil w dann dort ein Maximum annimmt, gilt . Andererseits folgt wegen aus Satz 3.2 , was ein Widerspruch ist. Also gilt w<M auf .

Die gleiche Methode läßt sich auch einsetzen, um Lemma 3.4 mit Hilfe von Lemma 3.3 zu beweisen: Falls ein Punkt entlang des Ellipsoid-Randes gefunden werden könnte, an dem w den Wert M annimmt, ließe sich eine Kugel finden, auf deren Rand w den Wert M an einem Punkt annimmt, der nicht ober- oder unterhalb des Mittelpunktes liegt, was im Widerspruch zu Lemma 3.3 stünde.

 

BEWEIS. Da und a beschränkt sind, gibt es reelle Konstanten und mit und . Sei die Elliptizitätskonstante von , d.h. für alle und für alle gelte . Wähle so klein, daß

Dies ist äquivalent zu

 

Aufgrund der Kleinheitsvoraussetzung an V, nämlich der Bedingung, daß V innerhalb des Streifens liegt, ist die Barrierenfunktion

für positiv in . Man rechnet nach:

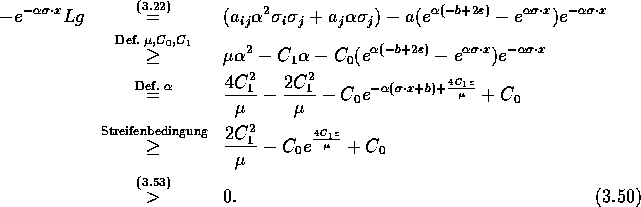
Setze

dann folgt

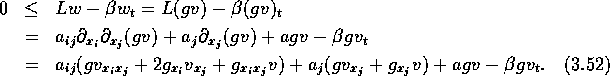
Nach Division durch g erhält man

Dies ist eine lineare Differentialungleichung für v. Im Innern, d.h. in V, kann v kein positives Maximum annehmen, denn dann müßte dort , und gelten, was wegen im Widerspruch zur Differentialungleichung stehen würde. Ebenfalls kann v auf kein positives Maximum annehmen, denn sonst würde an einem solchen Punkt gelten: und , was ebenfalls ein Widerspruch zur Differentialungleichung wäre. Auch Punkte des Neumannrandes sind für positive Maxima ausgeschlossen, denn Satz 3.2 würde dort implizieren. Wegen auf dem Dirichletrand folgt in und wegen g>0 auch .

 

BEWEIS. OBdA sei w<0 auf . Weiterhin kann durch entsprechende Wahl von so weit verkleinert werden, daß es der Kleinheitsvoraussetzung von Satz 3.5 genügt. Die Funktion

ist positiv in B und nimmt auf ganz den Wert 0 an. Man rechnet leicht

 

nach. Wie im Beweis von Lemma 3.3 kann so groß gewählt werden, daß

in , wobei ist.

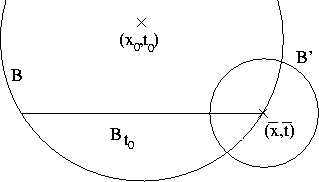
Auf der kompakten Menge gilt für ein geeignetes . Daher kann so klein gewählt werden, daß

auf nicht größer als 0 wird. Aus Satz 3.5 folgt dann auf . Demnach muß sein. Mit (3.62) folgt die Behauptung.

 

BEWEIS. Annahme: Die Behauptung ist falsch. Dann gibt es einen Punkt mit . Genau wie in Lemma 3.4 können wir annehmen, daß die Verbindungsstrecke ganz in V liegt. Es gibt ein , so daß ganz in V liegt und daß w<0 in gilt. Sei B' das Ballviertel, das in liegt und das dem Punkt zugewandt ist, d.h.

Lasse nun B' wie im zweiten Beweis von Lemma 3.4 durch Skalierung in Richtung wachsen, bis es einen Punkt auf dem Rand des entstehenden Viertelellipsoids gibt mit . Dies trifft spätestens dann zu, wenn das Viertelellipsoid den Punkt erreicht. Nach Wahl von stoßen wir dabei nicht an den Rand von V. Der Punkt muß auf dem gebogenen Teil des Viertelellipsoidrandes liegen, denn in gilt nach Wahl w<0. Im Punkt nimmt w ein Maximum an. Da dieser Punkt im Inneren von liegt, folgt . Andererseits gilt nach Satz 3.6 für einen hinsichtlich des Viertelellipsoids nach außen zeigenden Vektor . Dies ist ein Widerspruch, also muß die Annahme falsch sein.

  

BEWEIS. Der Beweis erfolgt in drei Teilen. Zuerst werden w und V durch Variablentransformationen und Gebietsverkleinerung geeignet zurechtgelegt. Dann wird eine Barrierenfunktion konstruiert, und im dritten Teil schließlich das eigentliche Maximumprinzip angewandt.

Teil 1: Wir nehmen an. Da die Hyperflächen von der Klasse sind, die Vektoren und auf in einer Umgebung von 0 linear unabhängig sind und und nicht senkrecht zur t-Achse liegen, gibt es einen -Diffeomorphismus der Form

der V in einer Umgebung transformiert in . Der Typ der Differentialgleichung bleibt dabei erhalten, ebenso die Bedingung (3.66), die sich jetzt einfacher schreibt als auf . Um die Notation zu vereinfachen, bezeichnen wir das neue Gebiet wieder mit V und behalten auch die alten Variablenbezeichnungen bei.

Aus Satz 3.7 folgt w<0 in . Durch eine weitere Transformation der Form

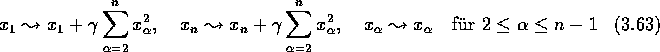
erreicht man, daß w<0 sogar in gilt, wobei das Gebiet V bei belassen wird. Bei dieser Transformation bleibt wie oben die Differentialgleichung erhalten, jedoch geht die Eigenschaft (3.66) verloren, da Teile des alten Gebietsrandes nicht mehr auf den neuen Gebietsrand abgebildet werden. Stattdessen gilt immerhin noch

für eine geeignete Konstante C>0.

Wir führen nun eine dritte Variablentransformation durch. Setze

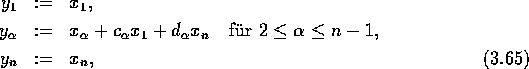
wobei die Variablen und noch bestimmt werden müssen. Für diesen Beweis sei die folgende Summationskonvention vereinbart: Über doppelt auftretende Indices i, j, k wird von 1 bis n summiert und über Indices von 2 bis n-1. Damit gilt

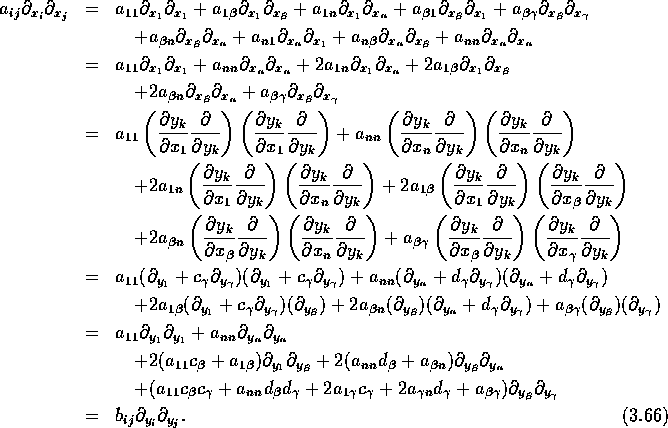
Wähle

dann gilt auf der t-Achse

Wie oben bezeichnen wir aus Gründen der Übersichtlichkeit die neuen Koordinaten im folgenden wieder mit . Wir erhalten somit nach allen Transformationen die Eigenschaften

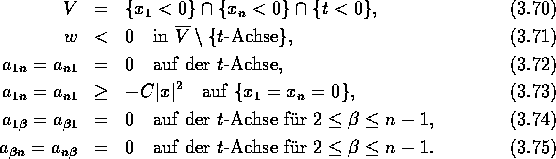
Teil 2: Sei M:=L-a der Operator L ohne den Term nullter Ordnung, d.h.

Wir betrachten die Funktionen

 

wobei die Konstanten k>0 und später gewählt werden. Aus z wird später die Barrierenfunktion gebildet. Man rechnet nach, daß z die Eigenschaften

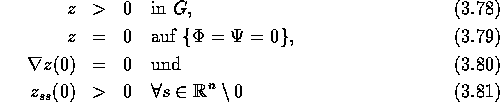
besitzt, wobei

sei. Es gilt

 

Für hinreichend großes ist

 

analog gilt eine Abschätzung . Schränkt man das Gebiet durch die Bedingung ein, so gilt auf unter der Voraussetzung

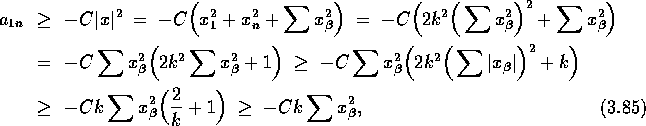
wobei C eine universelle Konstante ist. Aufgrund der Lipschitzstetigkeit der gilt , so daß wiederum unter der Voraussetzung gilt:

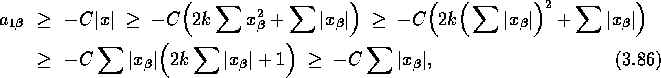
ebenso folgt . Damit gilt auf für hinreichend großes

 

Beschränkt man sich auf

für ein großes , so gilt in :

 

Wegen in gilt dort und somit

 

Der Mittelwertsatz der Differentialrechnung liefert uns für die Ungleichungen

Für gilt daher

Daher folgt in

für hinreichend großes aus (3.96) die Abschätzung

also . Mit Hilfe von z kann man nun die eigentliche Barrierenfunktion definieren:

Sei

Dann gilt in G' wegen t<0 und :

 

Wegen für ist

 

Somit gilt G' wegen für ein hinreichend großes

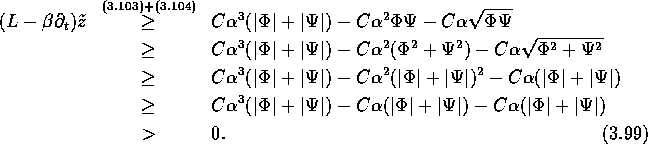
Teil 3: Diese Barrierenfunktion kann nun für das eigentliche Maximumprinzip genutzt werden. Sie hat folgende Eigenschaften:

1)

auf ,

2)

,

3)

,

4)

.

Die Transformationen aus Teil 1 führten zu w<0 in . G' ist wegen der Bedingung so geformt, daß w auf nur im Ursprung den Wert 0 annimmt. Ein Ball B um den Ursprung kann so klein gewählt werden, daß auf gilt. Auf der kompakten Menge gilt w<0, somit kann so klein gewählt werden, daß

dort nicht positiv wird. Auf dem verbleibenden Stück des Randes gilt nach Wahl von B. Somit gilt auf . Wende Satz 3.5 an (das Gebiet konnte durch hinreichend kleine Wahl von B vorher bliebig klein gemacht werden), und man erhält in .

Wegen v(0)=0 nimmt v sein Maximum in 0 an, also gilt für einen äußeren Vektor dort notwendigerweise . Falls sogar gilt, folgt wegen 2)

Anderenfalls gilt und damit notwendigerweise , da sonst kein Maximum vorliegen könnte. Mit 3) folgt