Zum Beweis wird die folgende Existenzaussage
aus der Funktionalanalysis verwendet:
Nun zum Beweis von Satz 4.5:
BEWEIS. Setze 
und
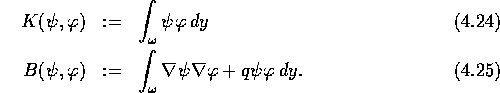
Trivialerweise ist K symmetrisch und positiv definit sowie B beschränkt und symmetrisch. Die
Vollstetigkeit von K wird durch den Satz von Rellich garantiert. Die Koerzivität von B sieht man folgendermaßen:
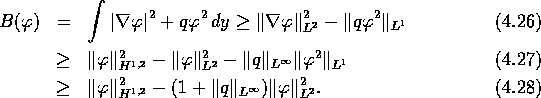
Somit sind die Voraussetzungen von Lemma 4.6 erfüllt, und es existieren ein
kleinstes 
und ein 
, die das Eigenwertproblem lösen. Gemäß dem
Regularitätssatz folgt
. Wegen 
für alle 
folgt mittels partieller Integration
Testet man mit 
, so ergibt sich bei der partiellen Integration der
zusätzliche Randterm 
. Wegen
(4.29) fallen die anderen Terme weg, so daß dieses Randintegral null ist, also
auf 
gilt. Wegen 
kann man durch Skalierung
noch 
erreichen.
Zu a): Mit 
ist auch 
Eigenfunktion zum Eigenwert , denn es gilt
und
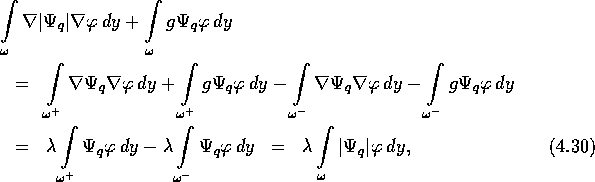
wobei 
und 
. Aus
dem Regularitätssatz folgt wie oben 
. Somit sind 
und 
Eigenfunktionen von der
Klasse 
zum Eigenwert . Setze
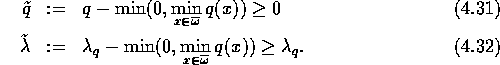
Damit gilt 
. Somit ist das Hopfsche
Maximumprinzip anwendbar, so daß gilt: Falls 
in 
oder auf
ein nichtpositives Minimum annimmt, dann ist konstant. Wegen , 
und 
folgt, daß 
strikt positiv und 
konstant null ist, also ist 
strikt positiv.
Zu b) und c): Teste mit 
in (4.23). Mit Hilfe von a) folgt
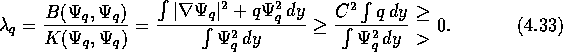
Zu d): Teste die schwache Formulierung des Eigenwertproblems zu 
mit und
integriere partiell:
Mit der Bezeichnung 
folgt
Wegen 
ist 
. Weil 
wie
bereits vorher festgestellt stetig in t ist (Bemerkung nach Gleichung
(4.6)) und wegen 
ist
stetig in t und nimmt für t=0 den Wert 0 an. Weil
an einer Stelle 
den Wert 1 annimmt und weil 
ist, gilt eine
Poincaré-Ungleichung für 
,
so daß gilt:
Zu e): Setze
Dann sind 
und 
charakterisiert durch
Es existieren Minimierer 
, also
Damit ist die Behauptung gezeigt.
