Zu 
sei 
der kleinste Eigenwert des klassischen
Eigenwertproblems
Die Existenz eines solchen Eigenwerts und der zugehörigen Eigenfunktionen wird im Abschnitt 4.3 behandelt. Setze
dann ist charakterisiert durch
hängt bzgl. der 
-Norm stetig von q ab. Daher ist
stetig in 
. Schreibt man das klassische und das verallgemeinerte Eigenwertproblem
untereinander,
so erkennt man, daß beide Probleme äquivalent sind, falls gilt:
Genau ist damit gemeint: Falls eine Lösung des verallgemeinerten Eigenwertproblems ist, so
ist 
eine Lösung des klassischen Eigenwertproblems. Falls
eine Lösung des klassischen Eigenwertproblems zu einem beliebigen 
ist und zusätzlich 
gilt, so ist eine Lösung des
verallgemeinerten Eigenwertproblems.
Bemerkenswert ist, daß die zugehörigen Eigenfunktionen bei beiden Problemen die gleichen sind, insofern übertragen sich sofort die bekannten Eigenschaften über Einfachheit und strikte Positivität/Negativität des Haupteigenwerts.
Im weiteren werden wir also nur noch die Gleichung (4.9) untersuchen.
BEWEIS. Für 
, 
und 
gilt
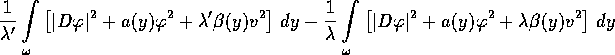
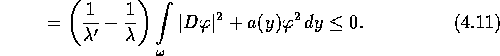
Die Monotonie überträgt sich auf 
.
BEWEIS. Zu sei 
die positive Eigenfunktion mit 
des klassischen Eigenwertproblems
Es gilt
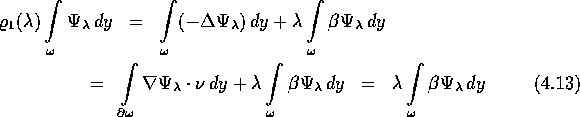
und somit
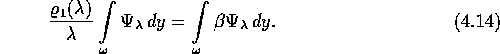
ist Eigenfunktion von 
. Weil 
in 
konvergiert für 
, folgt
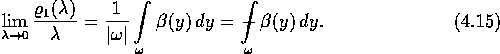
BEWEIS. 
ist nach Definition der kleinste Eigenwert von
Multipliziere diese Gleichung mit 
und integriere über 
auf:
Integriere den Term 
partiell. Nach Division durch 
folgt wegen 
:
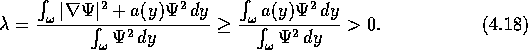
Nun kann Satz 4.1 bewiesen werden.
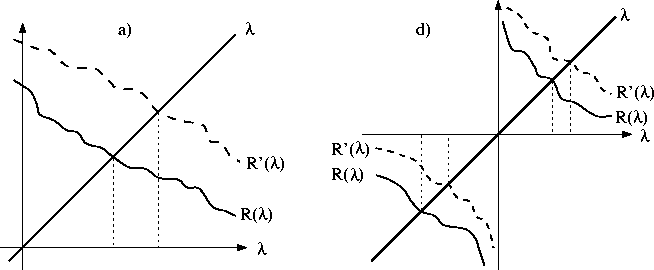
BEWEIS. a) Gemäß Lemma 4.3 ist die Funktion 
auf 
stetig und in
positiv. Da nach Lemma 4.2 monoton fallend ist,
nimmt diese Funktion auf 
nur positive Werte an, so daß es dort keinen Schnittpunkt mit der
Geraden 
geben kann. Auf der positiven Achse gibt es nach dem Zwischenwertsatz
einen Schnittpunkt (vgl. dazu auch die Abbildung). Offenbar ist dieser eindeutig.
b) Dieser Fall wird genauso wie a) bewiesen.
c) Gemäß Lemma 4.3 gilt R(0)=0. Aus Lemma 4.2 folgt,
daß 
auf 
und 
auf 
ist. Somit gibt es genau die Lösung
.
d) Lemma 4.4 zeigt 
. Somit gilt
Da die Funktion für 
stetig und gemäß Lemma 4.2 monoton
fallend ist, gibt es offenbar genau einen positiven und genau einen negativen Schnittpunkt.
e) Vom klassischen Eigenwertproblem wissen wir, daß 
gilt falls q<q'
ist. Für 
gilt also 
. Daraus folgt in den Fällen a) und d)
unmittelbar 
. Analog gilt für 
die Relation 
und somit 
. Daraus folgt in den Fällen b) und
d) sofort 
.
