Im folgenden wird der aktuelle Stand der Forschung in den von diesem Antrag berührten Forschungsgebieten im einzelnen in Kürze dargestellt.
Data Mining bzw. Knowledge Discovery oder auch Business Intelligence ist ein Prozess zum Auffinden von Mustern, Zusammenhängen und Trends in großen Datenbeständen wie sie sich in der Wirtschaft und der Forschung ergeben. Zum weiteren Umfeld des Data Mining gehört auch die anschließende Integration der Ergebnisse in die Geschäftsprozesse. Ziel des Data Mining ist es, neue, bisher verborgene und potentiell nützliche Informationen aus vorhandenen Daten zu extrahieren [7]. Data Mining wird heute hauptsächlich verwendet zur Klassifikation, z.B. zum Erstellung von (Kunden-)Profilen, zum Clustering, also zur Zerlegung von Datenbeständen in kleinere, homogene und zweckmäßige Teilmengen (Cluster) die bestimmte Eigenschaften teilen, und für Assoziationsanalysen (Sequenzanalysen), d.h. zur Bestimmung von Regeln die Zusammenhänge oder Muster beschreiben (Beispiel: Warenkorbanalyse, um Einkaufsverhalten zu erkennen).
Der Bereich der kommerziellen Anwendungen ist weit gestreut. Zu nennen wären auf Seiten der Wirtschaft beispielsweise die Prognose von Vertragskündigungen und Stornierungen, die Beurteilung von Kredit- und Antragsrisiken, Qualitätssicherung im Maschinenbau, Kundensegmentierung für Tarifgestaltung und die Erhöhung der Responserate beim Direkt-Mailing. Insbesondere im Zuge der Individualisierung des Massenmarketings kommt dem Data Mining eine Schlüsselrolle zu. Wissenschaftliche Anwendungen sind zum Beispiel die Auswertung von Daten in der Medizin (z.B. CT), die Gruppierung von Erdbebendaten, die Auswertung von Satellitenbildern, und auch die Auswertung der Daten von Observatorien.
Wichtige Data Mining Methoden sind Neuronale Netze [15], Entscheidungsbäume [5], Multivariate Adaptive Regressions Splines (MARS) [15], K-Nächste Nachbarn (k-NN) und Memory-Based Reasoning (MBR) [15], Clusterverfahren [5], Assoziationsverfahren, Support-Vector-Maschinen [18] sowie Regularisierungsnetzwerke [10].
Der eigentliche Data Mining Prozess läßt sich gemäß verschiedenen Modellen in einzelne Phasen einteilen. Im wesentlichen sind dies: die Vorbereitungsphase, die Phase der Aufbereitung der Daten, die Modellbildung (die eigentliche Mining-Phase), die Bewertungsphase und die Integration der Ergebnisse in den Geschäftsprozess.
Wir wollen uns auf die Modellbildung sowie die Bewertungsphase
konzentrieren.
Eines der Hauptprobleme beim Data Mining ist die Klassifikation von Daten.
Dabei wird nach einer Funktion ![]() (dem Klassifikator) gesucht,
die den vorgegebenen Daten jeweils eine bestimmte Klasse zuordnet
und somit Vorhersagen über die Klassenzugehörigkeit neuer Daten erlaubt.
(dem Klassifikator) gesucht,
die den vorgegebenen Daten jeweils eine bestimmte Klasse zuordnet
und somit Vorhersagen über die Klassenzugehörigkeit neuer Daten erlaubt.
Sei dazu
Nach eventueller Regularisierung kann die Klassifizierung oft als Interpolations-, Approximations- oder least square Aufgabe in hochdimensionalen Räumen aufgefaßt werden. In diesem Zusammenhang sind besonders Regularisierungs-Netzwerke [10] von Bedeutung, da sich die wichtigsten Neuronalen Netze, aber auch Support-Vector-Maschinen, als Regularisierungs-Netzwerke formulieren lassen [8]. Beim Ansatz des Regularisierungs-Netzwerks wird zur Kostenfunktion, die den Fehler bezüglich der Daten beschreibt, ein regularisierender Term addiert, der die Glattheit der resulierenden Approximierenden bestimmt. Es gilt
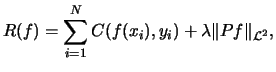 |
(1) |
Der Zusammenhang zwischen der Glattheit einer Funktion und dem Abfall ihrer Fourierkoeffizienten ist seit langem bekannt und es gelten ähnliche Zusammenhänge auch für nicht periodische Funktionen und deren Koeffizienten bezüglich anderer Multiskalenbasen [4,6]. In der Numerik wird dieser Zusammenhang in vielfacher Weise ausgenutzt, zum Beispiel bei der Konstruktion von Fehlerschätzern zur Steuerung adaptiver Verfeinerungen bei der approximativen Lösung von Operatorgleichungen [19] und auch bei der Konstruktion von optimalen Vorkonditionierern [6]. Eine zentrale Rolle spielt dieser Zusammenhang bei der Konstruktion von Algorithmen zur Approximation von Funktionen und zur Approximation von Lösungen von Differentialgleichungen, genauer bei der Auswahl geeigneter Approximationsräume und Basen. Bei einer schlechten Wahl der Approximationsräume (beziehungsweise der Basen) leidet die Approximationsordnung, was in der Praxis zu nur sehr langsam konvergierenden Verfahren, beziehungsweise - bei höherdimensionalen Problemen - zu Algorithmen mit zu hohen Anforderungen an Speicher- wie auch Rechenkapazitäten führt. Trotz der schnellen Entwicklung in der Computertechnologie sind in solchen Fällen viele Probleme einer direkten numerischen Simulation aufgrund ihrer hohen Komplexität nicht zugänglich. Das heißt, eine angemessene Genauigkeit erfordert zu viele Unbekannte, beziehungsweise der Aufwand pro Unbekannter ist zu groß.
Die Abhängigkeit des zur Lösung einer Operatorgleichung
nötigen Aufwands von der Raumdimension d
ist in erster Linie bestimmt durch die
Glattheit der beteiligten Funktionen (wie rechter Seite, Lösung und
eventueller Koeffizientenfunktionen). Ein typisches Glattheitsmaß ist hier gegeben durch
isotrope Sobolevräume.
Andere (stärkere) Glattheitsvoraussetzungen können die Abhängigkeit der Komplexität
von der Dimension verringern und eine approximative Lösung solcher Probleme wieder möglich
machen, indem Unterräume mit relativ großer Dimension,
die jedoch nur wenig zur Fehlerreduktion beitragen, identifiziert und aus
dem Approximationsraum weggelassen werden.
In Extremfällen lassen sich dann Algorithmen konstruieren, deren Kosten
zur Lösung bis auf ![]() -Genauigkeit asymptotisch unabhängig sind von der
Dimension des Problems [3].
-Genauigkeit asymptotisch unabhängig sind von der
Dimension des Problems [3].
Entsprechende Konstruktionen wurden auch bereits in
[1,16] unter dem Namen ``hyperbolisches
Kreuz''-Approximationsräume (auch
Dünne Gitter oder Boolsche Blending-Schemata)
eingeführt. In diesen Approximationsräumen ist die Zahl der
Freiheitsgrade gegenüber dem zugeordneten vollen Gitter
signifikant reduziert, von ![]() im Fall des vollen Gitters
auf
im Fall des vollen Gitters
auf
![]() im Fall des hyperbolischen Kreuzes (
im Fall des hyperbolischen Kreuzes (![]() : Level der
Diskretisierung,
: Level der
Diskretisierung, ![]() : Raumdimension). Gleichzeitig wird bei der
Approximation von Funktionen aus solchen Tensorprodukträumen
die Genauigkeit der
Approximation in Abhängigkeit von der Fehlernorm annähernd
aufrecht erhalten und dies trotz der erheblich verminderten
Anzahl der Freiheitsgrade, siehe zum Beispiel [17].
Damit wird das Verhältnis von Aufwand zu
Genauigkeit im Vergleich zu vollen Gittern erheblich verbessert
und der Aufwand zur Lösung von Differentialgleichungen
kann sehr stark reduziert werden [2].
: Raumdimension). Gleichzeitig wird bei der
Approximation von Funktionen aus solchen Tensorprodukträumen
die Genauigkeit der
Approximation in Abhängigkeit von der Fehlernorm annähernd
aufrecht erhalten und dies trotz der erheblich verminderten
Anzahl der Freiheitsgrade, siehe zum Beispiel [17].
Damit wird das Verhältnis von Aufwand zu
Genauigkeit im Vergleich zu vollen Gittern erheblich verbessert
und der Aufwand zur Lösung von Differentialgleichungen
kann sehr stark reduziert werden [2].