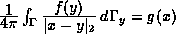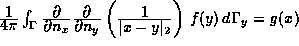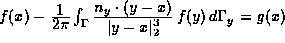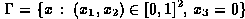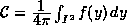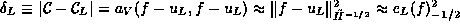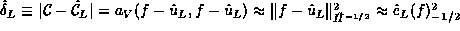|
Description
|
We are interested in the solution of boundary integral equations on a
two-dimensional manifold  in in 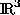 (screen problems). Here, we deal with the
single layer potential equation
(screen problems). Here, we deal with the
single layer potential equation
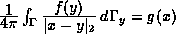
which we will write as operator equation Vf = g where V
is a pseudodifferential operator of order -1. This problem is equivalent
to the Dirichlet problem for the Laplace equation in the exterior domain
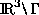 with Dirichlet data g on with Dirichlet data g on 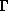 .
We are furthermore interested in the hypersingular equation .
We are furthermore interested in the hypersingular equation
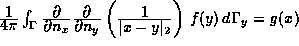
which we will write as operator equation Df = g where D
is a pseudodifferential operator of order 1, and in the
double layer potential equation
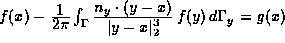
which corresponds to the interior Neumann problem.
We solve the integral equations with the BEM where we use semi-orthogonal
Riesz bases as ansatz functions as well as test functions (Galerkin method).
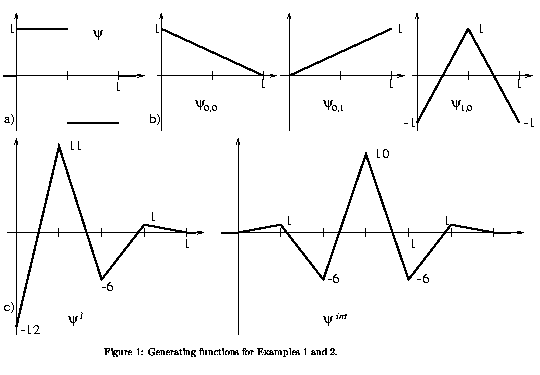
In the numerical tests we use two different examples for such Riesz bases:
- example 1: piecewise constant functions (Haar basis)
- example 2: semi-orthogonal linear spline wavelets
In the following, Figure 1 shows the generating functions for the
piecewise constant Riesz bases (Figure 1 a) as well as for the
semi-orthogonal linear spline wavelets (Figure 1 b,c). The grid point
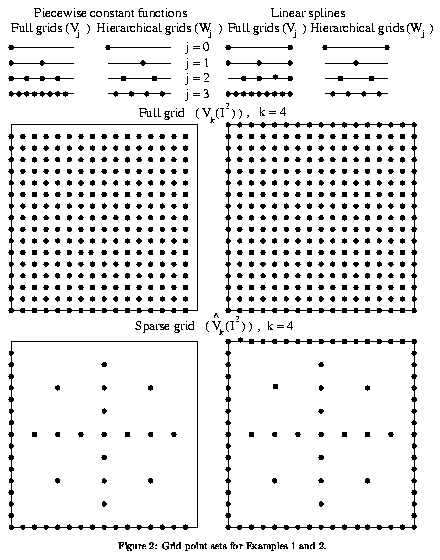
sets of both above examples of Riesz bases can be seen in Figure 2.
Here, the one-dimensional case is shown in the top of the figure. In the
middle of this figure the full grid case can be seen, while the sparse
grid case is presented at the bottom.
The discretization of each of the above integral equations leads to a
linear system of equations where the entries of the stiffness matrices
can be computed exactly using recurrence formulae which can be found
in [8]. Obviously, the resulting stiffnes matrices
are symmetric positive definite as we use the same bases for the ansatz
and test functions. Hence, we use the conjugate gradients method as an
iterative solver where we use Jacobian preconditioning.
We have run comparative test for both above mentioned Riesz bases. All
tests are for the capacity problem for a unit square screen with
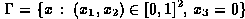
for the single layer potential equation with right hand side g=1, e.g.
we compute approximate solutions of the problem Vf=1. The capacity of
a screen is defined as the average of the solution f of the equation
Vf=1:
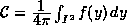
Let us denote by L the Level of the discretization (of a full grid and a
a sparse grid, respectively), and let 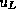 and and 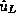 be the Galerkin solutions of the single layer potential equation for
the full grid space
be the Galerkin solutions of the single layer potential equation for
the full grid space 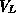 and the sparse grid space and the sparse grid space
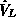 , respectively. It is well-known that , respectively. It is well-known that
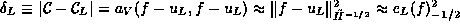
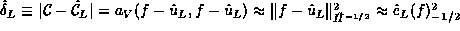
holds. Therefore, it is enough to concentrate on capacity errors.
In the following, some numerical examples are shown. In the tables
we use the abbrevations L for Level, K for kondition number of the
stiffness matrix, It for the number of iterations to reduce the
relative error by 10-6 in the residual of the preconditioned
system, E(C) for the capacity error and q for the quotient in the
capacity error showing the numerical convergence of the scheme.
First, the results obtained using the Haar basis are presented.
Table 1: Results for tensor product haar bases for
full grids (columns 2-5, first columns denoted by K/It/E(C)/q) and
sparse grids (columns 6-9, second columns denoted by K/It/E(C)/q)
| Level |
K |
It |
E(C) |
q |
K |
It |
E(C) |
q |
| 1 |
1.00 |
1 |
-0.030452 |
- |
1.00 |
1 |
-0.030452 |
- |
| 2 |
2.13 |
3 |
-0.016812 |
1.81 |
1.95 |
2 |
-0.016831 |
1.81 |
| 3 |
3.50 |
8 |
-0.009133 |
1.84 |
3.00 |
4 |
-0.009209 |
1.83 |
| 4 |
5.39 |
12 |
-0.004806 |
1.90 |
4.53 |
8 |
-0.004915 |
1.87 |
| 5 |
7.53 |
14 |
-0.002483 |
1.94 |
6.29 |
12 |
-0.002596 |
1.89 |
| 6 |
- |
- |
-0.001268 |
1.96 |
8.39 |
14 |
-0.001369 |
1.90 |
| 7 |
- |
- |
-0.000643 |
1.97 |
10.79 |
17 |
-0.000723 |
1.89 |
| 8 |
- |
- |
-0.000325 |
1.98 |
13.56 |
20 |
-0.000384 |
1.88 |
The results of Table 1 can also be seen in the following two figures
(Figure 1 and Figure 2) where the capacity error and the condition
number divided by L2 vs. degrees of freedom can be seen.
As the latter expression tends to a constant value, the condition
number of the stiffnes matrices is proportional to L2
for the Haar bases.
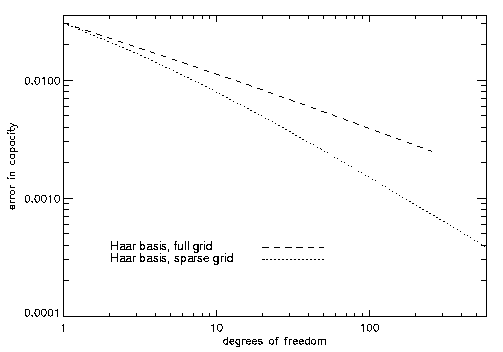 Figure 1: error in capacity vs. degrees of freedom
Figure 1: error in capacity vs. degrees of freedom
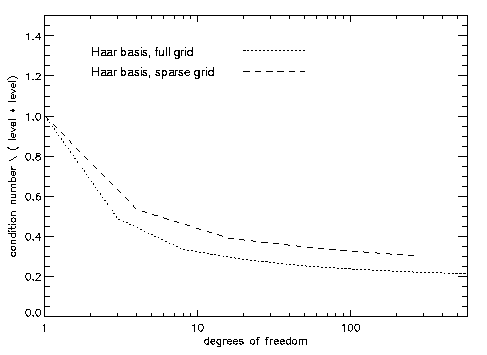 Figure 2: condition number / L2 vs. degrees of freedom
Figure 2: condition number / L2 vs. degrees of freedom
Let us now turn to the results one gets when taking the linear spline
prewavelts into account. Table 2 contains the numerical results, again
for the full grid case (columns 2-5) and for the sparse grid case
(columns 6-9).
Table 2: Results for tensor product linear
spline prewavelets for full grids (columns 2-5, first columns
denoted by K/It/E(C)/q) and sparse grids (columns 6-9, second columns
denoted by K/It/E(C)/q)
| Level |
K |
It |
E(C) |
q |
K |
It |
E(C) |
q |
| 1 |
1.00 |
1 |
-0.030452 |
- |
1.00 |
1 |
-0.030452 |
- |
| 2 |
35.47 |
3 |
-0.013142 |
2.32 |
35.42 |
2 |
-0.013216 |
2.30 |
| 3 |
40.18 |
6 |
-0.007785 |
1.69 |
40.12 |
4 |
-0.007839 |
1.69 |
| 4 |
42.12 |
9 |
-0.004113 |
1.89 |
42.72 |
7 |
-0.004173 |
1.88 |
| 5 |
- |
- |
- |
- |
44.32 |
9 |
-0.002169 |
1.92 |
| 6 |
- |
- |
- |
- |
45.29 |
10 |
-0.001120 |
1.94 |
| 7 |
- |
- |
- |
- |
45.88 |
11 |
-0.000577 |
1.94 |
The results of Table 2 can also be seen in the following two figures
(Figure 3 and Figure 4) where the capacity error and the condition
number vs. degrees of freedom can be seen. Here, we are almost in
the asymptotic range, and we already see that the condition number
is bounded from above as theory predicts.
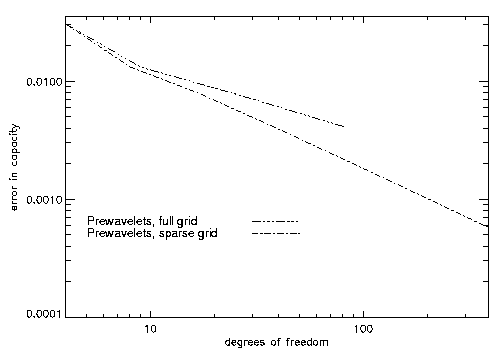 Figure 3: error in capacity vs. degrees of freedom
Figure 3: error in capacity vs. degrees of freedom
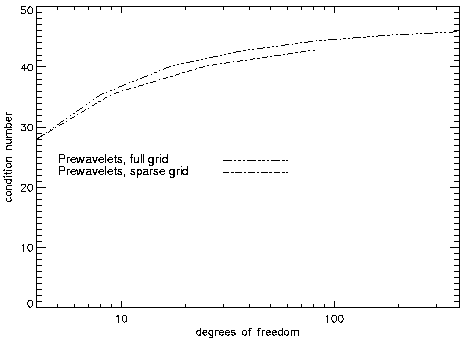 Figure 4: condition number / L2 vs. degrees of freedom
Figure 4: condition number / L2 vs. degrees of freedom
The solution of the equation Vf=1 has corner singularities as well as
edge singularities. Hence, adaptive refined grids instead of quasiuniform
ines are surely more apropriate, compare e.g. [7],
[9] and [10]. In the case of the
single layer potential equation the leading singular components of the
solution f are known. Hence, we use suitable regularized functions that
describes the behaviour of the leading singularity to generate an adaptive
sparse grid. The whole procedure as well as a regularized function can be
found in [2]. Grids obtained with the regularized
function in [2] can be found in Figure 5. Here, the maximum level of the
grids are 4, 12 and 21, and the corresponding number N of grid points is
57, 217 and 1841.
Figure 5: adaptive sparse grids obtained by the
regularized function (Lmax = 4, 12, 21, resp. N = 57, 217,
1841)
 |
 |
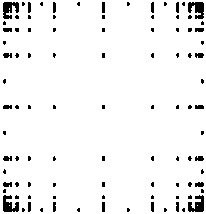 |
Taking the above adaptive sparse grids into account, the numerical
results using linear spline prewavelets for the Galerkin solution of
the single layer potential equation can be found in Table 3. Here,
Lmax deotes the maximum Level of a grid point in the adaptive
sparse grid and N denotes the number of grid points. Again, K denotes
the condition number, It the number of CG iterations to reduce the
relative error by 10-6 in the residual of the preconditioned
system, and E(C) is the capacity error.
Table 3: Results for tensor product linear
spline prewavelets for adaptive sparse grids
| Lmax |
N |
K |
It |
E(C) |
2 |
17 |
40.11 |
4 |
-0.007838 |
3 |
37 |
42.72 |
7 |
-0.004173 |
4 |
57 |
44.26 |
8 |
-0.002183 |
5 |
77 |
45.16 |
9 |
-0.001151 |
6 |
97 |
45.68 |
9 |
-0.000624 |
8 |
137 |
46.15 |
10 |
-0.000223 |
10 |
177 |
46.30 |
12 |
-0.000123 |
| Bibliography
|
- [1] C.K. Chui and J.Z. Wang,
On compactly supported spline wavelets,
Trans. Amer. Math. Soc. 330 (1992), pp. 903-915
- [2] M.Griebel, P. Oswald, T. Schiekofer,
Sparse grids for boundary integral equations,
Numerische Mathematik, submitted, 1998
- [3] M.Griebel, S. Knapek, T. Schiekofer,
Remarks on the compression of Galerkin discretizations of Pseudodifferential operators using wavelets of tensor product type,
in preparation
- [4] M.Griebel, S. Knapek,
Optimized approximation spaces for operator equations,
SFB 256 Report, 1998
- [5] N. Heuer, M. Maischak, E.P. Stephan ,
The hp-Version of the Boundary Element Method for Screen Problems,
Preprint, Institut für Angewandte Mathematik der Universität Hannover, 1997
- [6] W. Hackbusch
Integral Equations, Theory and Numerical Treatment,
Birkhäuser, Basel, 1995
- [7] H. Holm, M. Maischak, E.P. Stephan,
The hp-version of the boundary element method for Helmholtz screen problems,
Computing 57 (1996), pp. 105-134
- [8] M. Maischak,
hp-Methoden für Randintegralgleichungen bei 3D-Problemen, Theorie und Implementierung,
Dissertation, Institut für Angewandte Mathematik der Universität Hannover, 1996
- [9] M. Maischak, P. Mund, E.P. Stephan,
Adaptive multilevel BEM for acoustic scattering,
Preprint, Institut für Angewandte Mathematik der Universität Hannover, 1997
- [10] P. Mund, E.P. Stephan,
Adaptive two-level boundary element methods for the single layer potential
in
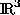 ,
Preprint, Institut für Angewandte Mathematik der Universität Hannover, 1997 ,
Preprint, Institut für Angewandte Mathematik der Universität Hannover, 1997
- [11] P. Oswald,
Nonlinear N-term approximation of singularity functions in two Haar Bases,
Preprint, Bell Labs, Lucent Technologies, 1998
| | Related projects
|
-
Compression of Galerkin discretizations of pseudodifferential
operators using wavelets of tensor-product type
(S. Knapek)
| |
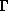 in
in 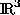 (screen problems). Here, we deal with the
single layer potential equation
(screen problems). Here, we deal with the
single layer potential equation