Performance-dependent options are financial derivatives whose payoff
depends on the performance of one asset in comparison to a set of
benchmark assets. Typically, the more benchmark assets are outperformed,
the higher the payoff will be. Performance-dependent options are interesting
for two reasons: one motivation is pure speculation (similar to horse races as
depicted in the picture to the left), the second application comes from the
hedging of bonus programs.
Companies make big efforts to bind their staff to them for longer periods
of time in order to prevent a permanent change of executives in important
positions. Besides high wages, such efforts are long-term incentive and bonus
schemes. One widespread form of such schemes consists in giving
the participants a conditional award of shares. If the participant stays
with the company for at least a prescribed time period he will
receive a certain number of company shares at the end of the
period. Typically, the exact amount of shares is determined by a performance
criterion such as the company's gain over the period or its ranking among
comparable firms (the peer group). This way, such bonus schemes induce
uncertain future costs for the company.
It is now a huge risk for a company to leave this position unhedged.
The company could buy the maximum number of possibly needed shares at
the starting time of the scheme. This, however, would require a large
withdrawal of funds from the company's capital that could be put to better use.
The purchase of vanilla call options on the maximum number of possibly needed
shares is a smaller but still overdimensioned trade.
The appropriate financial instruments in this case are so-called
performance-dependent options. Such options simply
include the performance criterion in their contract.
Using these options, the
company is able to purchase exactly the number of required shares at
the end of the scheme. Performance-dependent options minimize the amount of
money the company needs to hedge the future payments arising from the bonus
scheme. They can, when traded,
also be used for pure performance speculation purposes as a bet on the alpha
of a company or a fund manager (alpha certificates). This way profits can be
realized independently of the trend of the market.
In this project, we aim to define a framework for the efficient valuation of
fairly general performance-dependent options.
Thereby, we assume that the performance
of an asset is determined by the relative increase &Delta S = S(T) / S(0)
of the asset price over the considered period of time.
This performance is then compared to the
performances of a set of n-1 benchmark assets and saved in a vector Rank(S) ∈ { +, - }n
which contains n plus or minus signs and depends on the joint distribution of all
stock prices S = ( S 1 , ... , S n ).
A plus sign in the first component indicates that the stock price of our company is above the strike and
a plus sign in i-th component denotes that company i (which is the
(i-1)-th benchmark company) has been outperformed.
For each possible outcome R ∈ { +, - }n of the ranking
bonus factors, aR finally define the payoff of the option to its
holder. The payoff of the performance-dependent option at time T is
then given by
We use a multidimensional Black-Scholes model
for the temporal development of all asset
prices required for the performance ranking.
If the number d of stochastic
processes in the model equals the number n of companies we speak of a full
model. In the case d < n, we call the model reduced.
Reduced models arise by grouping companies to sectors or
via principal component analysis of full models.
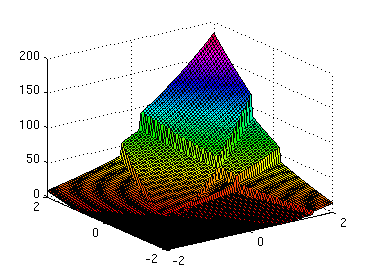
A performance depending option with 5 companies which pays a bonus which
increases linearly with the number m of outperformed benchmark companies is defined for instance
by the bonus factors
aR=m/4.
In this case the payoff thus only depends on the number of plus signs in the ranking
vector aR which defines the rank of our company in the benchmark.
If the company ranks first there is a full payoff
(S1(T) - K)+. If it ranks last, the payoff is zero.
The payoff of this option in case of a reduced model with two
stochastic processes X1 and X2 is displayed in the figure above.
Note that the payoff function is typically divided into several regions where
each region corresponds to a different ranking. Between these regions the payoff
function is discontinuous due to the jumps in the bonus factors.
The structure of the discontinuities in the payoff function above is displayed in the figure left.
One can see that the underlying geometry is described by an hyperplane arrangement which contains
n=5 (hyper-) planes in the d=2 dimensional space.
Within the above setting the martingale approach yields the fair price of the
performance-dependent option as a
multidimensional integral whose dimension is the number of stochastic processes
used in the model. Unfortunately, in the full-model case as well as in
the reduced one there is no direct closed-form solution for this
integral. Moreover, the integrand is typically
discontinuous which makes accurate numerical solutions difficult to achieve.
In this project, we investigate the derivation of closed-form solutions
to these integration problems.
Our general approach is to decompose the integration domain into regions
where the payoff function is smooth (see the figure above).
While these regions, which are defined by the underlying hyperplane arrangement,
are easily found in the full model case, tools
from computational geometry have to be used in the
case of reduced models. Moreover, the integration regions may be
defined by general polyhedra in the d-dimensional space.
To handle this more complicated geometry we decompose the regions
further into simple so-called orthant regions.
This is possible by using exactly one orthant per polyhedron as illustrated in
the figure to the right for a hyperplane arrangement with three planes. Here, three polyhedra
P1, P2 and P3
are decomposed into a signed sum using the three orthants
O1, O2 and O3.
This strategy not only works in the shown two-dimensional example but also for general dimensions and an arbitrary number of benchmark companies. The decomposition algorithm is based on the Lawrence signed decomposition lemma and uses the fact that every hyperplane arrangement can be decomposed into orthants by using exactly one orthant per cell.
These valuation formulas can be seen as multivariate generalizations of the classical Black-Scholes formula for performance-dependent options. In practice, the formulas allow a fast end efficient computation of option prices even for large benchmarks.